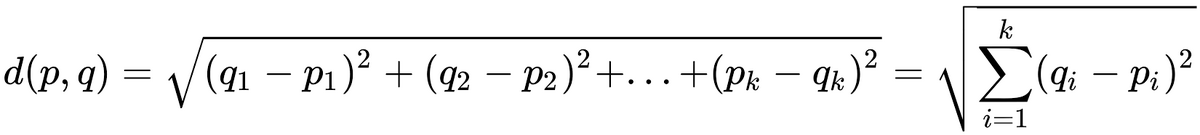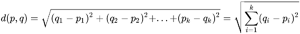Q: Do higher-dimensional entities automatically get Immeasurable speed?
A: No. To put it simply: Although the presence of the additional axis results in a higher-dimensional space being infinitely larger in comparision to a lower-dimensional one, the numerical values themselves remain unchanged, as a "dimension" is nothing more than a continuum of numbers representing a direction of space. Consequently, the euclidean distance between a Point A and a Point B is always represented by an one-dimensional path (Regardless of the dimension of the space in which they are embedded), whose length is always measurable and given by a generalization of the
Pythagorean Theorem to n dimensions. That is:
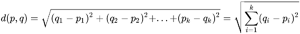
Or, in plain english: Subtracting each of the coordinates of the starting and ending points (Distance is always given by the
absolute value, so whether the result is negative or not is irrelevant), squaring the results, summing them up, and then taking the square root of the resulting value.
So, for example, in two-dimensional space, the distance between the points (4,4) and (8,8) is calculated through the following formula:
d(4,8) = |√(4 – 8)² + (4 – 8)²|
d(4,8) = √4² + 4²
d(4,8) = √16 + 16
d(4,8) = √32
d(4,8) = √32 = 5.656854 ≈ 6
Then, to generalize this to higher dimensions, we only have to take into account the additional variables. For example, in 6-dimensional space, the distance between the coordinates (2,2,2,2,2,2) and (8,8,8,8,8,8) is:
d(2,8) = |√(2 – 8)² + (2 – 8)² + (2 – 8)² + (2 – 8) + (2 – 8)² + (2 – 8)²|
d(2,8) = √6² + 6² + 6² + 6² + 6² + 6²
d(2,8) = √36 + 36 + 36 + 36 + 36 + 36
d(2,8) = √216 = 14.6969384567 ≈ 15
Taking the "15" to be some arbitrary unit of distance, it is then perfectly possible to gauge a defined speed for a character who crosses it in a given length of time. For example, if 15 in this case is 15 meters, then a character who crosses this in a second would naturally be moving at 15 m/s
Similarly, moving in a higher-dimensional space also doesn't qualify as Immeasurable speed, and would be more appropriately rated as
Interdimensional range
Of course, this formula doesn't always illustrate how the distance between two points works in real life, as the Earth has curvature and is obviously not a perfectly flat plane like Euclidean Space (At least non-locally), and the same applies to the universe at large. This is no issue, however, as there are plenty of metrics that can be applied to non-euclidean spaces: For example, the distance between two points on the surface of a sphere is given by a
geodesic, as opposed to a straight line passing directly through the sphere's interior, whose length is itself given by its
spherical distance.
They can qualify for Immeasurable Speed, however, if the regular dimension of time appears like a spatial dimension from their higher dimensional perspective. That is to say, that it can freely be traversed both forward and backwards, allowing them to access any point in it and move unbound by the notions of time inherent to the lower space. An example of this are the
Bulk Beings from Interstellar.