• This forum is strictly intended to be used by members of the VS Battles wiki. Please only register if you have an autoconfirmed account there, as otherwise your registration will be rejected. If you have already registered once, do not do so again, and contact Antvasima if you encounter any problems.

    For instructions regarding the exact procedure to sign up to this forum, please click here.
  • We need Patreon donations for this forum to have all of its running costs financially secured.

    Community members who help us out will receive badges that give them several different benefits, including the removal of all advertisements in this forum, but donations from non-members are also extremely appreciated.

    Please click here for further information, or here to directly visit our Patreon donations page.
  • Please click here for information about a large petition to help children in need.

Ben 10 - Low 1-C Time Stream Proposal

Status
Not open for further replies.
DarkGrath said:
In comparison to the whole Time Stream that Ben and Maltruant Fly through, the Space Beyond is infinitesimal. Can I get more context on this? Watching the clips provided, I don't see where this is confirmed. I don't see the Space Beyond that they travel through even referenced in the clip where they travel through the Time Stream; I suspect there's just some context not given from this clips that explains this away, but I need to understand this in more depth before I can agree with it.
Click to expand...
The Time Stream is a higher dimensional cylindrical structure that contains the Space Beyond within its walls.
 
Firestorm808 said:
The Time Stream is a higher dimensional cylindrical structure that contains the Space Beyond within its walls.
Click to expand...
I see. And what of the relative size? Is the Time Stream infinite in length? And how does its size compare to the Space Beyond within its walls?
 
Not getting a room to give counter argument or anything seems kinda...
836385441992146945.png
 
Personally unsure at the moment. The gist of this is that since there's a space quantifiably larger than a "2-A universe", it must be of a higher dimension? And because a 2-A structure is, by definition, infinite 4-D then there shouldn't be anything 2-A that is also larger than infinity? And that the size of the 2-A structure implies that there's a 5th axis from which the cluster can be viewed as finite? Sounds fine in theory, but then any cosmology with multiple 2-A structures should, by that logic, be Low 1-C, no? But instead that wouldn't even be considered a larger 2-A (which can be established, even if illogical). I may have missed something, but this seems to be having your cake and eating it too.

Can you expand more on the black space being infinitesimal in comparison to the timestream?
 
Just to clarify for everyone here, the discussion on whether or not universes in Ben 10 are 2-A is actually still on going

Zamasu brought up a debunk thread to counter this, he brought up good points to refute this idea and I still plan to continue the thread for this.
 
ProfessorKukui4Life said:
Just to clarify for everyone here, the discussion on whether or not universes in Ben 10 are 2-A is actually still on going

Zamasu brought up a debunk thread to counter this, he brought up good points to refute this idea and I still plan to continue the thread for this.
Click to expand...
I see, the thread was open for more than 3 months without inputs and zamasu then suddenly left, in anycase this thread is not concerned with that.
 
ProfessorKukui4Life said:
Just to clarify for everyone here, the discussion on whether or not universes in Ben 10 are 2-A is actually still on going

Zamasu brought up a debunk thread to counter this, he brought up good points to refute this idea and I still plan to continue the thread for this.
Click to expand...
it isn't at the moment, the thread closed
 
GyroNutz said:
Sounds fine in theory, but then any cosmology with multiple 2-A structures should, by that logic, be Low 1-C, no?
Click to expand...
Uh, no. Having multiple 2A is stated in our FAQ to be nothing more than 2A, as one infinity can contain other infinity w/o being bigger than that.
The reason is that the total amount of universes contained in a collection of multiple infinitely-sized multiverses (even one consisting of infinitely many of them) is in fact equal to the amount of universes contained in a single one of the multiverses that form this ensemble: It is countably infinite, as the union of countably-many countable sets is itself countable, and thus does not differ in size from its components.
Click to expand...
 
GyroNutz said:
The gist of this is that since there's a space quantifiably larger than a "2-A universe"
Click to expand...
Also the point is that 2A universe is just a countable infinite and very first thing that can be bigger than this is uncountable infinite, there is nothing in between countable infinite and uncountable infinite (natural numbers and real numbers) unless a verse establish so. Which infact is as well accepted to be low 1C in FAQ and space beyond views these 2A structures as nothing more than tiny stars.
 
ProfessorKukui4Life said:
Just to clarify for everyone here, the discussion on whether or not universes in Ben 10 are 2-A is actually still on going

Zamasu brought up a debunk thread to counter this, he brought up good points to refute this idea and I still plan to continue the thread for this.
Click to expand...
Uh wait, I am being told off site that after being opened for months and when zamasu left after telling that he will reply we close the thread that no one is opposing and i made this thread (which I was planning to do but was on hold because of zamasu), you want to continue the thread right now in the middle of my crt? I must be misunderstanding.
 
Reiner said:
Uh wait, I am being told off site that after being opened for months and when zamasu left after telling that he will reply we close the thread that no one is opposing and i made this thread (which I was planning to do but was on hold because of zamasu), you want to continue the thread right now in the middle of my crt? I must be misunderstanding.
Click to expand...
Continue THAT thread? Not necessarily. But the points Zamasu brought up being continued in a new thread or being mentioned here (which is very much on topic as this entire upgrade solely relies on the idea that all universes in Ben 10 contain infinite universes)? Yes. Whatever comes first.

I don’t know exactly what went on here with Zamasu and y’all as I was away from the wikia for sometime, but everyone has different situations to deal with in their personal lives to step away for any length of time they want or need. Just because I was absent when Zamasu decided to leave doesn’t mean me or someone else who agrees with his take cannot continue what was left off.
 
GyroNutz said:
Personally unsure at the moment. The gist of this is that since there's a space quantifiably larger than a "2-A universe", it must be of a higher dimension? And because a 2-A structure is, by definition, infinite 4-D then there shouldn't be anything 2-A that is also larger than infinity? And that the size of the 2-A structure implies that there's a 5th axis from which the cluster can be viewed as finite? Sounds fine in theory, but then any cosmology with multiple 2-A structures should, by that logic, be Low 1-C, no? But instead that wouldn't even be considered a larger 2-A (which can be established, even if illogical). I may have missed something, but this seems to be having your cake and eating it too.
Click to expand...
@GyroNutz , this is the idea behind the thread (and has been used previously for many verses), Natural numbers contains even numbers and odd numbers but yet aren't bigger than them but equal as we aren't jumping any higher but just adding more elements in the same size of space and it's even mentioned in The FAQ:
This illustrates some of the more unintuitive properties of sets with infinite elements: Namely, given a set X, it being a subset of another set Y does not imply that Y > X in terms of size. An example of this is how the set of all natural numbers contains both the odd numbers and even numbers, yet all of these sets in fact have the same number of elements.
Click to expand...

But as there is no way to reach any higher or bigger than the countable infinite by the methods I mentioned above like multiplying, divide or what not. We use the idea in Set theory of Power set of set is greater than the set. That said infinities uses the same method to jump higher over countable infinite and reach another infinite uncountable infinite (aleph1). So very first thing that is bigger than countable infinity is uncountable infinite which is low 1C when is over a 2A structure. The point that space beyond sees those structures just as tiny stars basically fits the discription.
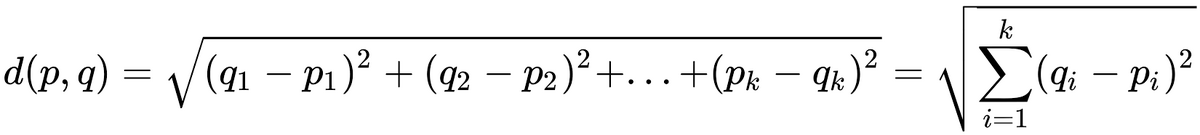
vsbattles.fandom.com

Tiering System FAQ

A: Whether higher-dimensional entities qualify for such high tiers or not depends on several different factors, which may take root both in and out-of-verse. To explain this situation, we must first clarify what exactly being higher-dimensional entails. In a way, yes, though not how most would...
vsbattles.fandom.com vsbattles.fandom.com

There is really no such thing as finitely or countable infinite bigger than 2A and so difference is uncomfortable which is Low 1C as per standards, said by Ultima:

That comparision doesn't really work here, because if you considered a "transcendence" descriptor as actually indicating some form of superiority in size that is capable of being given the same tier as the space being transcended, then you could as well just give it Low 1-C, since 2-A is in itself a tier indicating a structure whose (4-dimensional) volume is already ∞, and so there is really no such thing as being finitely or countably infinitely bigger than it, as the current standards on affecting multiple infinite multiverses attest to. The difference needs to be uncountable, one way or another. "At least 2-A" would be the absolute least you could choose. ~said by ultima This thread
Click to expand...

Also proceeding further,

Kevin: Where are we? There is nothing on my instruments.

Professor paradox: There is nothing outside either, Do you see that thin glow?

Gwen: A star?

Professor paradox: Actually, it's the universe. We are in the space beyond.

This entire conversation supports that universes are insignificant comparison to space beyond that professor paradox just straight out said there is nothing outside but when goes a bit in conversation, said that there is but just too small to notice or mention normally, space beyond is largely empty and by far bigger than those universes and it is supported by the visuals as well.
 
Last edited:
My opinion is unchanged, to use this form of argument you must prove that the difference between the countable infinite structure and the other elements is akin to that of uncountable infinite. Just because the element is outside the structure does not prove that they are bigger, such as with how the likes of the intergers or rational numbers are no greater than the natural numbers.

You need to have evidence of a qualitative difference. No matter what form of argument you mean, no matter what sciences you bring. A qualitative difference is as important to reaching Tier 1 as Cantor's diagonal was to proving uncountable infinite exists and that the nature of the real numbers was different to that of the rational numbers.
 
Everything12 said:
Just because the element is outside the structure does not prove that they are bigger,
Click to expand...
It is literally bigger tho, entire seen is screaming for it. They're tiny stars in it, they're thin glow and insignificant to be noticed + supported by visuals which are literal. The idea of integers having odd numbers and natural numbers is only valid when the size of the structures are same. Of which there is no evidence but contradict the context.

Literally everyone here has no problem with space beyond being bigger than the universe as it is obvious.
 
Last edited:
Reiner said:
It is literally bigger tho, entire seen is screaming for it. They're tiny stars in it, they're thin glow and insignificant to be noticed. The idea of integers having odd numbers and natural numbers is only valid when the size of the structures are same. Of which there is no evidence but contradict the context.
Click to expand...
Appearing as tiny stars is not evidence of a qualitative difference. The difference between countable and uncountable infinity is so much greater than that.

Also, Integers are not odd and even (though they do contain them), they are positive (natural numbers) and negative and zero.
 
Everything12 said:
Appearing as tiny stars is not evidence of a qualitative difference.
Click to expand...
It is? Regardless of what you add to infinite or just keep adding infinite or multiply it. You'll never reach beyond it, never go beyond it. Only way is to go uncountable which is low 1C as per our FAQ.
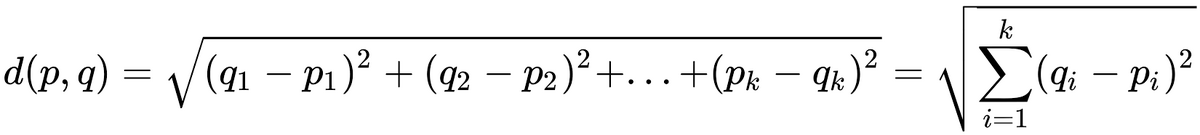
vsbattles.fandom.com

Tiering System FAQ

A: Whether higher-dimensional entities qualify for such high tiers or not depends on several different factors, which may take root both in and out-of-verse. To explain this situation, we must first clarify what exactly being higher-dimensional entails. In a way, yes, though not how most would...
vsbattles.fandom.com vsbattles.fandom.com
Everything12 said:
Also, Integers are not odd and even (though they do contain them), they are positive (natural numbers) and negative and zero.
Click to expand...
I know? Did i say they're same? I said their sizes are same regardless if one contains the other. Natural numbers can never be bigger than odd numbers.
 
Reiner said:
It is? Regardless of what you add to infinite or just keep adding infinite or multiply it. You'll never reach beyond it, never go beyond it. Only way is to go uncountable which is low 1C as per our FAQ.
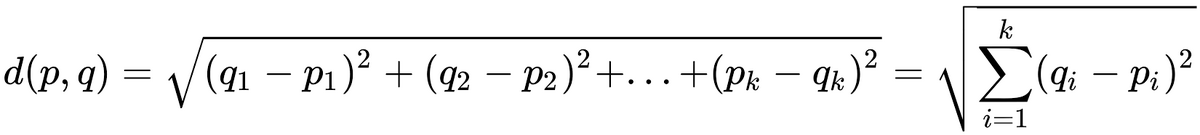
vsbattles.fandom.com

Tiering System FAQ

A: Whether higher-dimensional entities qualify for such high tiers or not depends on several different factors, which may take root both in and out-of-verse. To explain this situation, we must first clarify what exactly being higher-dimensional entails. In a way, yes, though not how most would...
vsbattles.fandom.com vsbattles.fandom.com
Click to expand...
Are the integers outside the natural numbers? Are the integers bigger than the natural numbers?
 
Natural numbers - odd numbers
1 - 1
2 - 3
3 - 5
And so on. One can keep going but there will always be a one element in odd number for all elements of natural numbers. And hence number of elements are same, one is not bigger than another.
 
Also that I am being asked to prove stuff like, prove that the difference between the size of space beyond is uncountable infinite when I have already done it? It seems to be there is a misconception that uncountable infinite is infinitely larger countable infinite when it is not, there is no such thing as bigger than countable infinite by countable infinite times. Uncountable infinite is simply the seconds largest infinity just after countable infinite. That's it, there is no size comparison known. How much bigger is uncountable infinite comparison to countable infinite? We don't know but we do know that uncountable infinite is indeed larger that's it, saying countable infinite times bigger than countable infinite is just.... Doesn't right. It's just another infinite.
The set of real numbers has minimal possible cardinality which is greater than the cardinality of the set of integers. That is, every set, S, of real numbers can either be mapped one-to-one into the integers or the real numbers can be mapped one-to-one into S. As the real numbers are equinumerous with the powerset of the integers,
{\displaystyle |\mathbb {R} |=2^{\aleph _{0}}}
and the continuum hypothesis says that there is no set
S
for which
{\displaystyle \aleph _{0}<|S|<2^{\aleph _{0}}}
.
Click to expand...
 
Last edited:
Reiner said:
Also that I am being asked to prove stuff like, prove that the difference between the size of space beyond is uncountable infinite when I have already done it? It seems to be there is a misconception that uncountable infinite is infinitely larger countable infinite when it is not. Uncountable infinite is simply the seconds largest infinity just after countable infinite. That's it, there is no size comparison known. How much bigger is uncountable infinite comparison to countable infinite? We don't know but we do know that uncountable infinite is indeed larger.
Click to expand...
It's true that uncountable infinity is so unbelievable big that it's hard to actually get a grasp on how big it is.

However we do know what the real numbers that are uncountable infinite are; that being every number on the number line including decimals, so we do have somewhat of an idea of how big it is and it's not a complete unknown. With it being something like infinity ^ infinity, and that's how the likes of the wiki treats it.
 
Last edited:
Reiner said:
Just bigger than countable infinite, nothing more nothing less is all that is known.
Click to expand...
We do know that the real numbers are uncountable infinity, so that's what we use as a measuring stick to prove if something has the qualitive difference to be uncountable infinite.
 
Everything12 said:
infinity ^ infinity
Click to expand...
Just saw the edit. And then again, we don't know it's value and how big infinity^infinity is from infinity. As in the end it'll just break of in infinite*infinite*.....-infinite. so it's just unknown. We just treat it as real numbers are bigger than natural numbers and Power set of set is greater than set. We have idea of it being bigger as it cannot be reached by just simply multiplying infinities or what not, in the end just being significantly bigger is all.
As I quoted above, real numbers contains minimal greater cardinality than natural numbers.
 
We know that the natural numbers are countable infinite.

We know that despite having additional elements, that the integers and rational numbers are not greater than the natural numbers and are also countable infinity.

We know that the real numbers are greater than countable infinity; uncountable infinity.

We know that the real numbers are every number on the number line including decimals; giving them a size like infinity ^ infinity, because their is a whole lot of decimal numbers between even 0 and 1.

Thus uncountable infinity equals a value equal to the real numbers. That is the logic the wiki uses.

Reiner said:
Just saw the edit. And then again, we don't know it's value and how big infinity^infinity is from infinity. As in the end it'll just break of in infinite*infinite*.....-infinite. so it's just unknown. We just treat it as real numbers are bigger than natural numbers and Power set of set is greater than set. We have idea of it being bigger as it cannot be reached by just simply multiplying infinities or what not, in the end just being significantly bigger is all.
As I quoted above, real numbers contains minimal greater cardinality than natural numbers.
Click to expand...
True that infinity ^ infinity is a value so great that it's hard to grasp it, but we have a vague idea of what it means, and that vague idea is close to our understanding of how big the real numbers are. So that's what we use. That's just what you got to deal with when you got something as large as uncountable infinity.
 
Last edited:
Reiner said:
Just bigger than natural numbers 🗿
Click to expand...
Well it is 0 and 0.1 and 0.01 and 0.001 and 0.0001 and 0.00001 and 0.000001 and 0.0000001... then we got 0.11 and 0.111 and 0.1101 and 0.11001... and somewhere after that we have 0.2 and all the stuff that comes after that, until we get to 1 and then we do the same thing for every decimal between 1 and 2, and then their all the decimal place between all the other countably infinite natural number, then we include all the countable infinite negative numbers and the decimals between them as well.

So while we don't have a concrete list of how large the real numbers and all it's decimals are, no one has the time or brainpower for that, we do at least have an idea.

Said idea is close to what we think infinity ^ infinity would be. So that's the comparison we use. And as the real numbers are uncountably infinite, that's what we use as the value you need to be equal to be considered uncountable infinite.
 
Status
Not open for further replies.

Similar threads

Hellformer
Ben 10: Minor Additions/Upgrade
2 3
Replies
80
Views
3K
Hellformer
Hellformer
Reiner04
  • Locked
Ben 10: Re-justification of Low 1-C.
2 3
Replies
91
Views
8K
Georredannea15
Georredannea15
Reiner04
  • Locked
Ben 10: Crosstime Possibly Low 1-C re-justification.
6 7 8
Replies
284
Views
18K
Reiner04
Reiner04
Ghengiroo115
Ben 10: Low 5-B downgrade/reinterpretation
2
Replies
60
Views
3K
omegabronic
omegabronic
REX9097
  • Locked
Ben 10 Cosmology Upgrade
Replies
19
Views
1K
Firestorm808
Firestorm808
Back
Top