• This forum is strictly intended to be used by members of the VS Battles wiki. Please only register if you have an autoconfirmed account there, as otherwise your registration will be rejected. If you have already registered once, do not do so again, and contact Antvasima if you encounter any problems.

    For instructions regarding the exact procedure to sign up to this forum, please click here.
  • We need Patreon donations for this forum to have all of its running costs financially secured.

    Community members who help us out will receive badges that give them several different benefits, including the removal of all advertisements in this forum, but donations from non-members are also extremely appreciated.

    Please click here for further information, or here to directly visit our Patreon donations page.
  • Please click here for information about a large petition to help children in need.

The Problem with Storm/Clouds Calculations

Status
Not open for further replies.
Might as well generalize to a spherical cap formula, given that I think it isn't as complicated as I initially though.

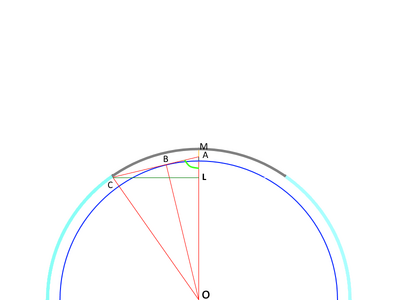
Let R be planet radius, h be observer height, H be cloud height and T be cloud Thickness.

As reasoned above the distance along the ground is R*arccos(R/R+h) + R*arccos(R/R+H).


In the following we wish to model things as a Spherical sector (That will spare us intergrating over a spherical cone).

For that purpose we wish to know half the cone angle, which we name phi (i.e., the angle between the rim of the cap and the direction to the middle of the cap as seen from the sphere center, to quote wikipedia)

phi (in radians) = 2*pi * (R*arccos(R/R+h) + R*arccos(R/R+H) / 2*pi*R) = arccos(R/R+h) + arccos(R/R+H)

as (R*arccos(R/R+h) + R*arccos(R/R+H) / 2*pi*R) is the precentage of our distance from the whole planet circumference.


Now H high above our earth surface is the base of the clouds. Hence the Volume of stuff between the cloud base and earth's center is given by the Volume of the spherical cap with radius R+H and half the cone angle phi.

Volume of this spherical sector should be (as per wikipedia):

V1 = 2/3 * pi * (R+H)^3 * (1-cos(phi))


Now directly above the surface of the spherical sector we just modeled is another T meter of clouds. The Volume between the top of the clouds and the center of earth should be a spherical sector with radius R+H+T and half the cone angle phi.

Hence it's Volume is:

V2 = 2/3 * pi * (R+H+T)^3 * (1-cos(phi))


The Volume covered by clouds is exactly the difference between V2 and V1 then:

V2 - V1 = 2/3 * pi * (R+H+T)^3 * (1-cos(phi)) - 2/3 * pi * (R+H)^3 * (1-cos(phi))

= 2/3 * pi * (1-cos(phi)) * ((R+H+T)^3 - (R+H)^3)

= 2/3 * pi * ( 1-cos( arccos(R/R+h) + arccos(R/R+H) ) ) * ((R+H+T)^3 - (R+H)^3)

= 2/3 * pi * ( 1- (R/R+h)*(R/R+H) + sin(arccos(R/R+h))*sin(arccos(R/R+H)) ) * ((R+H+T)^3 - (R+H)^3)

= 2/3 * pi * ( 1- (R/R+h)*(R/R+H) + sqrt(1-(R/R+h)^2)*sqrt(1-(R/R+H)^2) ) * ((R+H+T)^3 - (R+H)^3)

Where from the 3rd into the 4th row the addition theorem for cosinus was used and from the 4th into the 5th row the identity sinus(x) = sqrt(1-cos(x)^2).


So Cloud Volume = 2/3 * pi * ( 1- (R/R+h)*(R/R+H) + sqrt(1-(R/R+h)^2)*sqrt(1-(R/R+H)^2) ) * ((R+H+T)^3 - (R+H)^3)


... right?


That aside, again my question: Would Visibility usually be a concern for us?
 
Looks fine but use forgot to add parentheses since devision goes before addition. So

Cloud Volume = 2/3 * pi * ( 1- (R/(R+h))*(R/(R+H)) + sqrt(1-(R/(R+h))^2)*sqrt(1-(R/(R+H))^2) ) * ((R+H+T)^3 - (R+H)^3)

I'll try to come up with a simplier formula though
 
Volumeformulae
Here we have 2 right triangles.

AB = Sqrt((R+h)^2 - R^2)-Sqrt((R+H)^2 - R^2) via Pythogorean theorem.

Area of a spherical cap is 2*pi*R*h

Where R - raduis of the earth + clouds height. h - LM (see the picture above)

LM = AL-h+H for obvious resons

AL = Sqrt((R+h)^2-R^2)+Sqrt((R+H)^2-R^2)*cosÔêáA

cosÔêáA = Sqrt((R+h)^2-R^2)/(R+h)

so height of the spherecal cap = (Sqrt((R+h)^2-R^2)+Sqrt((R+H)^2-R^2))*(Sqrt((R+h)^2-R^2)/(R+h))+H-h

Area of the sperical cap = 2*pi*(R+H)*((Sqrt((R+h)^2-R^2)+Sqrt((R+H)^2-R^2))*(Sqrt((R+h)^2-R^2)/(R+h))+H-h)

Now we can multiply in by thickness of the clouds to find volume:

V = T*2*pi*(R+H)*((Sqrt((R+h)^2-R^2)+Sqrt((R+H)^2-R^2))*(Sqrt((R+h)^2-R^2)/(R+h))+H-h)
 
Okay this doesn't look any simplier

But height of the spherical cap can be easily calculated here

Distance = R*arccos(R/R+h) + R*arccos(R/R+H)
 
DontTalkDT said:
That aside, again my question: Would Visibility usually be a concern for us?
Click to expand...
I don't think that it usually is. When a calc uses the horizon distance, it's because you can clearly see the clouds reaching that far
 
Cloudscalcs2
Anyway, i tried to calculate it myself and found this:

Distance = AB = AH + BH

AH = R + H

BH = R + h

CH = R

AH = sqrt(AC^2-CH^2) = sqrt(R^2+H^2+(2*R*H)-R^2) = sqrt(H^2+2*R*H)

BH = sqrt(BC^2-CH^2) = sqrt(R^2+h^2+(2*R*h)-R^2) = sqrt(h^2+2*R*h)

AB = sqrt(H^2+2*R*H) + sqrt(h^2+2*R*h)

For the volume, we could use a cylinder as an approximation. So basically take this calculator, use cloud thickness as height, and the distance found previously as the radius

Sorry if maybe you already dicussed that, but i wasn't quite understanding the discussion above
 
Is spherical cap actually accurate though? I'm sure it only works if you assume the base of it is a straight line, which isn't going to be the case when you're dealing with something that follows earth's curvature, you're probably better off just modeling the cloud as a cylinder using the calculated distance as radius and standard cloud height.
 
Actully I think we got away from the topic.

My main point was that distance to the visible clouds should be determined as distance to the horizon from height of the observer + distance to the horizon from height of the clouds. Characteristic altitude of each type of clouds should be added here.

The way to determine volume of the visible clouds should be up to the person who does the calc.

Does anyone disargee?
 
I do agree that it should be determined this way, I thought the debate now was about finding a general formula for the total distance
 
Kaltias said:
I do agree that it should be determined this way, I thought the debate now was about finding a general formula for the total distance
Click to expand...
Now I think it should be determined the same way as before (assuming a cilinder). It turns out that the curvature is not as significant as I thought it would be and calculating volume of the spherical cap leads to even greater inaccuracy
 
We should also need to modify the cloud chart thingy. To list the altitude of different cloud types if that's possible.
 
It's not a percentage. A recalc is needed, it isn't the same as the standard cumulonibus height going down to 8 km, where we could simply take the original value multiplied by 8 and divided by 13
 
Sigurd Snake in The Eye said:
Will all the storm cloud calcs need to be changed?
Click to expand...
Not all of them, but the vast majority uses the old method to calculate the horizon, those will change
 
RebubleUselet said:
Schnee One said:
Is there a percentage on how much this increases the Potency of storms?
Click to expand...
I have the exact same question
Click to expand...
If you scroll up you can see me recalculating Thrall's storm feat. So basicly CAPE method results went up from Low 7-B+ to 7-A while KE method went up from High 7-A to Low 6-B+.
 
Bucko

Do you have any idea how many verses I'm in on that rely on storm calcs
 
Kaltias said:
@Ant

Probably both of them
Click to expand...
Is somebody knowledgeable willing to update them in a relatively easy to understand manner?

DontTalkDT is likely the most experienced in this area.
 
No no no man

There's also

Ninjago

RWBY (Which probably won't change honestly)

Mortal Kombat

And even Jack of All Tra-

.... Why do I keep bringing up my own works all the time
 
Not really

This is a horizon change

The horizon was already calculated to get what we have today
 
RWBY is actually unaffected by this, the horizon wasn't visible to begin with.

Anyway let's focus on updating the calc pages for now
 
Status
Not open for further replies.

Similar threads

CNBA3
Speed to cut clouds?
Replies
5
Views
332
CNBA3
CNBA3
Flashlight237
Storm Calculation Issues
Replies
9
Views
1K
Dalesean027
Dalesean027
Energy needed for destroy a celestial spherical object
Replies
16
Views
1K
Kudekuba
Can the Cloud Vaporization formula be used on physical attacks that have no signs of cloud Vaporization?
Replies
0
Views
160
M2u12
Armorchompy
  • Locked
Possible revision of our vision range/"twinkle in the sky" feats
2 3
Replies
86
Views
5K
Agnaa
Agnaa
Back
Top