The problem with angular size formulas

[Spinosaurus75DinosaurFan]

Sure go ahead.

 

[AguilaR101]

I am still confused as to why the formula uses panel height as opposed to width, isn't the FoV supposed to be horizontal?, if so it would make more sense to divide the object size by the width.

Also, why is 70┬░ the standard assumption?

According to this you should be able to find either Vertical or Horizontal FoV by utilizing the formulas outlined there.

 

[Ugarik]

No. I don't know why 70 is the standart assumption but vertical FoV makes as much scence as horizontal.

And you can't use those formulas either because you need to assume horizontal FoV in order to find vertical and vice versa.

 

[AguilaR101]

No. I don't know why 70 is the standart assumptio

I guess that's fine, but what do you mean by the latter part?

but vertical FoV makes as much scence as horizontal.

More or less I can infer that one can figure out angular size of an object by knowing how much of your field of view obstructs, thing is I find odd that the formula utilizes the height of the screen as opposed to the width since we are utilizing the horizontal field of view.

I'm referring specifically to this

2*atan(tan(70/2)*(object height/panel height))

And you can't use those formulas either because you need to assume horizontal FoV in order to find vertical and vice versa.

I noticed that after I actually checked them, derp.

 

[Ugarik]

Minecraft has 70 degrees vertical FoV by default. I guess that's where it comes from

 

[Lightbuster30]

I'm trying the calculation with degrees and I still get the results in radians (it says radians at the bottom of the screen), do I convert to degrees or?

 

[Lightbuster30]

Ignore this question. Just tested out Ryu's One Punch Man cloud hole calc by converting my rads to deg and got the same results he did. Guess I answered my own question.

 

[Antvasima]

Is there anything left to do here?

 

[Firestorm808]

@Antvasima

This is quite an old thread, but I'm wondering about the change in formula and use. From what I've seen in Lina's testing, the degree Angsizing formula doesn't match the testing in comparison to the radian formula. Has anyone else done similar testing with the same results?

2atan(tan(70deg/2)*(504px/980px)) = 39.6085798975 degrees which gives 0.527 m vs the actual 0.8 m

Angsizing

vsbattles.fandom.com

 

[Antvasima]

I do not remember this thread well anymore. Can you summarise what is suggested here please? I can call some knowledgeable members if necessary.

 

[DontTalkDT]

@Antvasima

This is quite an old thread, but I'm wondering about the change in formula and use. From what I've seen in Lina's testing, the degree Angsizing formula doesn't match the testing in comparison to the radian formula. Has anyone else done similar testing with the same results?

2atan(tan(70deg/2)*(504px/980px)) = 39.6085798975 degrees which gives 0.527 m vs the actual 0.8 m

Angsizing

vsbattles.fandom.com

That isn't really a matter of testing. The math looks like this:

So I managed to remember the maths I did




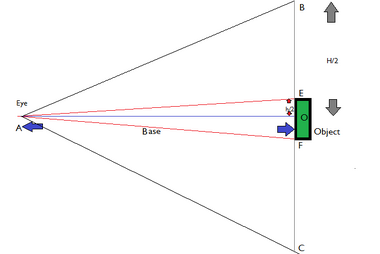
In the above very rough diagram, H is panel height (BC), h is object height (EF). The angle BAO will be half of a human eye's range of view (The range is 70 degree I believe).

In triangle BAO,

-Tan 70/2=(H/2)/Base

In triangle EAO

-Tan(x/2)=(h/2)/Base

If we divide the two equations

-h/H=Tan(x/2)/Tan(70/2)

Bringing tan70/2 to the left side

-Tan(70/2)*(h/H)=tan(x/2)

Using inverse

-Tan-1{Tan(70/2)*(h/H)}=x/2

-Or 2Tan-1{Tan(70/2)*(h/H)}=x

x is the angle you are supposed to find

I am fairly certain that the FoV was not intended to be 70 radians, as that is equal to 4010.7°, but 70°.

What the experiment is concerned, all that finds is that Lina's camera probably has a viewing angle of around 50° (=4010 modulo 360). An iphone on the other hand would have a 65° angle for their cameras (unless they changed that by now), which would be closer to the 70° figure.

Those things can vary within a certain natural looking range, which is why angsizing is not the most reliable of practices.

 

[Antvasima]

Thank you for helping out DontTalk.

 

[Yar_R_agi_7k]

For instance, if you were doing a calc for a Quake game, you should use 90 degrees instead of 70 degrees if you didn't change it to a value other than the default.

thanks for the advice

 

[Antvasima]

@DontTalkDT @Agnaa

So what should we do here?

 

[Agnaa]

I'm not sure, idk anything about the actual mathematical side of things, but for how to fix it, I still stand by my previous suggestion of checking over old angsizing calcs, commenting if they're still valid to avoid doubling up on work, and remaking incorrect ones.

 

[Antvasima]

Okay. So do we need to change our written standard instructions anywhere?