The Problem with Storm/Clouds Calculations

Ugarik · Nov 26, 2018

There is a huge problem with clouds measurements using distance to the horizon.

We currently use distance to the horizon to calculate volume of the clunds in cases when the clouds obscure the entire sky. The distance to the horizon is determined by this formula:

S = Sqrt((R+h)^2 - R^2)

Where R is the radius of the planet (6371000m for the Earth) and h is the height of the observer above the ground.

The problem with using distance to the horizon to determine area/volume of the clouds is the fact that are high in the sky which means EVEN IF THE CLOUDS ARE FURTHER THAN THE HORIZON THEY STILL WHOUD BE VISIBLE depending how high they are above the groud. I'll explain it in the image below:

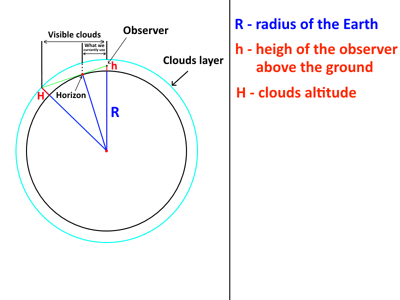
By Pythagorean Theoreme the correct formula to determine the distance to the furthest visible clouds is:

Sqrt((R+h)^2-R)+sqrt((R+H)^2-R)

Where R is the radius of the Planet, h is the height of the observer above the ground and H is the clouds altitude.

Since the area of the visible clouds will always be quite large we should probably always assume spherical cap shape insted of cilinder.

Mr. Bambu · Nov 27, 2018

I'm sorry, what are you trying to say? Try to avoid typos, I mean no offense it's just genuinely difficult to see what your point is.

Antvasima · Nov 27, 2018

You should invite the calc group members and DontTalkDT to discuss this issue: VS Battles Staff

Ugarik · Nov 27, 2018

Mr. Bambu said:
I'm sorry, what are you trying to say? Try to avoid typos, I mean no offense it's just genuinely difficult to see what your point is.

I'm saying that if the clouds obscure the entire sky we should use different formula to measure volume of the visible clouds insted of using distance to the horizon as raduis of a cilinder.

For example let's take this calc:

https://vsbattles.fandom.com/wiki/User_blog:Myriadofmemes/Warcraft_-_Thrall's_thunderstorm

The distance to the horizon at 17.08 altitude was calculated to be 14700 m. But the problem is that distance to the horizon does not determine raduis of the visible clouds. Since the storm was presumably created with cumulonimbus clouds their altitude should be 460 meter abouve the ground. The correct formula (as I've already explained it above) to determine radius of the visible clouds should be

14700+sqrt((6371000+460)^2-6371000^2) = 91260 m.

Since this is a desently large distance we should use area of a spherical cap S = 2pi*R*h

R = radius of the Earth + altiture of the clouds = 6371460 m.

h = height of the cap = (91260*(14700/(6371000+17.08))+460-17.08 = 653.49 m.

S = 2*pi*6371460*653.49 = 26161206900.1 m^2

Ricsi-viragosi · Nov 27, 2018

Pretty much, the clouds are higher, so they can be seen at a higher distance then a horizon?

Somewhat of a normie for this stuff, but that should be the gist of it, right? Wouldn't this enflate the feats to the point that they became extremly outlierish in most cases?

EmbalmerMaster9000 · Nov 27, 2018

If I'm understanding correctly, it takes into account how far someone is (assuming they're in the dead center of the clouds, I'm guessing) from the circumference of the clouds, thus changing the value based on such?

I suppose that it could be usable if we are given an exact cloud type/can guess one for a calculation in question. The horizon method wouldn't exactly be incorrect either depending on the scenario (E.G., seeing clouds past the horizon; it would be a lowball, but it might not take into account the height of the clouds thus be lower than it would w/o said values).

Ugarik · Nov 27, 2018

Ricsi-viragosi said:
Pretty much, the clouds are higher, so they can be seen at a higher distance then a horizon?

Somewhat of a normie for this stuff, but that should be the gist of it, right? Wouldn't this enflate the feats to the point that they became extremly outlierish in most cases?

Regarding the Thrall's storm feat

Low-End - 26161206900*13000*1.003*2500 = 8.52789*10^17 J - 203.82 Megatons (Mountain level)

High-End - 26161206900*13000*1.003*4000 = 1.36446*10^18 J - 326.11 Megatons (Mountain level)

So the feat went from Small City level+ to Mountain level. So it only all outlier depending to the context

Kaltias · Nov 27, 2018

I get the horizon stuff, but why we should assume a spherical cap?

A cylinder makes more sense

RKGenki · Nov 27, 2018

Maybe he meant a spherical shell? Because I can see why it would make sense

Andytrenom · Nov 27, 2018

If I'm understanding correctly, we now also need to know the height of clouds from ground in order to make calculations right?

Andytrenom · Nov 27, 2018

@Ricsi Even it does make many feats an outlier, that's not really a reason to reject the revision.

Ricsi-viragosi · Nov 27, 2018

Andytrenom said:
@Ricsi Even it does make many feats an outlier, that's not really a reason to reject the revision.

Oh, that's not what I'm saying. I'm just saying that if it does get implemented it should be taken into acount that it can lead to outliers.

Mr. Bambu · Nov 27, 2018

I mean

Our current method just low-balls

Which is what we normally do anyways

Not even sure this is needed

Kaltias · Nov 27, 2018

He is saying that the current method is wrong.

The horizon calculator gives you a shorter radius compared to what you can actually calculate

Ugarik · Nov 27, 2018

Ricsi-viragosi said:
Somewhat of a normie for this stuff, but that should be the gist of it, right? Wouldn't this enflate the feats to the point that they became extremly outlierish in most cases?

However if we apply KE method to the calc above:

KE = 0.5*26161206900*13000*1.003*(91260/9)^2 = 1.75367041*10^22 J - 4.19 Teratons (Small Country level+)

So KE method should probably go into a trashcan

Ugarik · Nov 27, 2018

Zanybrainy2000 said:
If I'm understanding correctly, it takes into account how far someone is (assuming they're in the dead center of the clouds, I'm guessing) from the circumference of the clouds, thus changing the value based on such?

I suppose that it could be usable if we are given an exact cloud type/can guess one for a calculation in question. The horizon method wouldn't exactly be incorrect either depending on the scenario (E.G., seeing clouds past the horizon; it would be a lowball, but it might not take into account the height of the clouds thus be lower than it would w/o said values).

The horizon method is only correct if the clouds are on the ground level which is abviously can not be true. So we should use average altitude of the given cloud type (460 meters for storm/cumulonimbus clouds)

Ugarik · Nov 27, 2018

Mr. Bambu said:
I mean

Our current method just low-balls

Which is what we normally do anyways

Not even sure this is needed

Distance to the horizon from 2 meter height should be about 5000 m. Height of the storm clouds is about 460 m from the ground level. That means coulds whould be 460 meters above the horizon which gives us angular size of Atan(0.5├ù5000├ù460)=2.63 degrees

Just for the comparosing angular size of the sun is 0.5 degrees which means you can fin 5 suns detween the horizon and the storm clouds. So we can't use it even as a lowball

Mr. Bambu · Nov 27, 2018

In OP the main issue seems to be that for very, very high altitudes, clouds would still be visible. I assume this is brought up because it would inflate results, and yet this method is laughably, ridiculously higher.

Also, I believe on an accurately scaled Earth it would appear less pronounced of an issue.

I'll just wait for other calc group members. As it stands I don't much see the point for most storm calcs.

Ricsi-viragosi · Nov 27, 2018

As Andy said, whenever or not outliers are made or not doesn't matter. Using wrong math to make a fear not an outlier doesn't work after all.

At most storm calcs become like creating matter.

Ugarik · Nov 27, 2018

Mr. Bambu said:
In OP the main issue seems to be that for very, very high altitudes, clouds would still be visible. I assume this is brought up because it would inflate results, and yet this method is laughably, ridiculously higher.

Not really. Those high altitudes clouds are Cirrus, Cirrocumulus and Cirrostatus. Those clouds never get in a lagre groups and can never obscure the entire sky (at least in real world). You can never see them near the horizon either because they simply become too small for you to see them

Ugarik · Nov 27, 2018

Mr. Bambu said:
Also, I believe on an accurately scaled Earth it would appear less pronounced of an issue.

No. Proportions will change but my formula remains the same. Pythagorean theorem still works and can be applied in this situation

Andytrenom · Nov 27, 2018

Should this be highlighted?

Ugarik · Nov 27, 2018

I think so

Antvasima · Nov 27, 2018

It is much better to just invite all of the calc group members, Kaltias, and DontTalkDT. They are the ones who should decide issues like this.

Ugarik · Nov 27, 2018

I also made a picture how the horizon would look during 10 km wide storm. Eye altitute is 2 meter which gives up distance to the horizon of 5 km (the same as the radius of the storm). Angular size atan(460/5000) = 5.26 degrees

Andytrenom · Nov 27, 2018

Wait...is it possible to calc the the cloud radius in cases where the clouds ''don't'' go beyond the horizon with this method?

Ugarik · Nov 27, 2018

Andytrenom said:
Wait...is it possible to calc the the cloud radius in cases where the clouds don't go beyond the horizon with this method?

It's not possible. I used the same radius as the distance to the horizon and calculated angular size using height of the clouds (460 m). You can't use this method if the clouds are any closes or further to the hozison.

Kepekley23 · Nov 27, 2018

I always wondered about the accuracy of the horizod method, since the average storm is roughly 24km in diameter and we had 99% of the storms in fiction only 1/5th that wide, but I never quite caught this problem specifically.

It's basically the same reason why distant mountains don't appear to extend to the horizon when seen from even dozens of kilometers away.

Ugarik · Nov 27, 2018

Well my point is that actual distance to the visible clouds is much higher that the distance to the horizon

Kepekley23 · Nov 27, 2018

That's what I said, though.

Kepekley23 · Nov 27, 2018

This also makes more than half of the storm calcs ever into outliers, too. Because it's a pretty massive boost.

Antvasima · Nov 27, 2018

Has somebody invited DontTalkDT yet?

Ugarik · Nov 27, 2018

I had but he hasn't responded yet

Antvasima · Nov 27, 2018

Okay.

DontTalkDT · Nov 27, 2018

I am not unaware of this. Cloud height in fiction isn't the most consistent thing, though, which is why I usually prefer not to assume it.

I guess we can make explicit mention of it on the page.

For that sake the formula R*arccos(R/R+h) + R*arccos(R/R+H) is more appropiate, I think.

If we approximate the clouds as cylinder for simplicity it gives a better result to use the distance along the earth curvature instead of the straight line between observer and observed. The formula above results from the formula already on the page and this consideration.

(I am also not quite sure where your formulas come from or if they are correct.)

That aside, this made me think about something. Should we consider this?

Kepekley23 · Nov 27, 2018

It isn't consistent, but neither is real life. There would be no reason for us to pin solid estimates if we could dismiss them all just because "fiction is inconsistent".

I'm personally not comfortable at all with ignoring more factual formulas just because they give off greater results than we personally would like the feats to be at.

Ugarik · Nov 27, 2018

DontTalkDT said:
For that sake the formula R*arccos(R/R+h) + R*arccos(R/R+H) is more appropiate, I think.

This formula will give you absolutely the same result. The only diffrience is the Sqrt((R+h)^2-R^2)-sqrt((R+H)^2-R^2) doesn't involve trigonometry and only uses simple Pythagorean theorem.

EDIT: Nevermind, your formula calcutates distance on the curved surface, while mine as a straight line

Jobbo · Nov 28, 2018

Bump.

Andytrenom · Nov 28, 2018

>I'm personally not comfortable at all with ignoring more factual formulas just because they give off greater results than we personally would like the feats to be at.

I'm not sure if Don'tTalk was actually suggesting that.

Kepekley23 · Nov 28, 2018

Not exactly, but close enough.

The Problem with Storm/Clouds Calculations

Suffer-Not-Injustice Bambu

Maintenance worker

Suffer-Not-Injustice Bambu

Suffer-Not-Injustice Bambu

Maintenance worker

Maintenance worker

Maintenance worker

A Fossil at This Point

Similar threads