-
This forum is strictly intended to be used by members of the VS Battles wiki. Please only register if you have an autoconfirmed account there, as otherwise your registration will be rejected. If you have already registered once, do not do so again, and contact Antvasima if you encounter any problems.
For instructions regarding the exact procedure to sign up to this forum, please click here. -
We need Patreon donations for this forum to have all of its running costs financially secured.
Community members who help us out will receive badges that give them several different benefits, including the removal of all advertisements in this forum, but donations from non-members are also extremely appreciated.
Please click here for further information, or here to directly visit our Patreon donations page. -
Please click here for information about a large petition to help children in need.
The Problem with Destruction Values We Use (Staff only)
- Thread starter Ugarik
- Start date
- Status
- 32,835
- 38,108
- 648
- 97
I guess I should've been more specific as to what constitutes a "big gun." Basically you can't kill an elephant with a 9mm glock, with the exception that you are really lucky and shoot right at a weak spot of the skull right into the brain or something like that. The same would apply to a robot though.
This is less important, but I want to clarify that if the robot doesnt have a weak spot, then that's not really a fair comparison. What counts as "more damage" or "less damage" also largely has to do with where the damage is done. If theres no weak spots, you cant really fairly compare it. DDM's point was that objects handle being penetrated better than others because of hardness and not dura, but in this case it's not about hardness but rather about the presence or lack thereof a weak spot. Two different things.
DDM, also by hardness, do you mean how durable a chunk of a character is compared to a chunk of the other character that is the same size? Basically durability density?
This is less important, but I want to clarify that if the robot doesnt have a weak spot, then that's not really a fair comparison. What counts as "more damage" or "less damage" also largely has to do with where the damage is done. If theres no weak spots, you cant really fairly compare it. DDM's point was that objects handle being penetrated better than others because of hardness and not dura, but in this case it's not about hardness but rather about the presence or lack thereof a weak spot. Two different things.
DDM, also by hardness, do you mean how durable a chunk of a character is compared to a chunk of the other character that is the same size? Basically durability density?
- 32,835
- 38,108
Hardness is the ability to resist scratching last I checked. Toughness is what determines how much energy it can take before penetration is imminent
Also you can kill an elephant with something waaaaaaaaay weaker than a 9mm, you can kill one with a 22 LR through the head but it's not gonna be humane in the least bit.
Also you can kill an elephant with something waaaaaaaaay weaker than a 9mm, you can kill one with a 22 LR through the head but it's not gonna be humane in the least bit.
- 31,442
- 34,274
A bullet would simply bounce off a plate of Titanium or Iron, and also durability in general isn't linear for different reasons. Copper normally isn't as durable as steel, but it requires more energy to fragmentation among other things. penetration is due to the sharpness of the object which harder objects are inherently sharper but not always tougher. Sharpening a sword too much actually makes it more breakable.
- 10,786
- 1,635
I mean like pascals.KLOL506 said:
- 10,786
- 1,635
In practice, most people would be in the same tier, the only ones who would change much are large and small size users, and weapon users. OK, that second one is pretty big.
- 10,758
- 6,491
So, reminder on what we're going to do with pulverisation feats?
- 32,835
- 38,108
If the current system stays, pretty much nothing.
If it doesn't, we need to figure out other stuff like area of effect and force first. Which would basically mean restarting the wiki from scratch. Simply using toughness isn't gonna cut it then. Though pulverization feats involving pressing into a wall and creating a smooth crater would be fine regardless.
If it doesn't, we need to figure out other stuff like area of effect and force first. Which would basically mean restarting the wiki from scratch. Simply using toughness isn't gonna cut it then. Though pulverization feats involving pressing into a wall and creating a smooth crater would be fine regardless.
- 32,835
- 38,108
I don't think we'll be able to simply use powder factor for rocks and stick with our current system for other materials at the same time for the reasons Bambu noted, not to mention powder factor is plenty tough enough to use as is, and that powder factor would wield more or less the same results as our current system.
Also area of effect and force will prolly never see the light of day due to what Assalt said.
Also area of effect and force will prolly never see the light of day due to what Assalt said.
- 31,442
- 34,274
DontTalk is still quite busy by the looks of it.
- 10,893
- 12,312
When asked about the destruction values I said before that I don't really know either. I'm not very knowledgable on these engineering topics.
Soooo... I can't really give much valuable input on this. I guess it probably makes sense.
One question I have: This is uniaxial compressive stress in the videos. Would something like punching a hole in the ground not be more triaxial compressive stress?
In any case I'm with Antvasima on the fact that we can, from a practicle perspective, not apply this anytime soon.
Soooo... I can't really give much valuable input on this. I guess it probably makes sense.
One question I have: This is uniaxial compressive stress in the videos. Would something like punching a hole in the ground not be more triaxial compressive stress?
In any case I'm with Antvasima on the fact that we can, from a practicle perspective, not apply this anytime soon.
- 1,178
- 407
- Thread starter
- #262
Yes, this method work for insolated chunks only. In fast punching a hole in the ground is way more complicated .DontTalkDT said:
- 302
- 46
Powder Factors would apply only to explosions involving rock. Fragmentation would reduce things to an average of ~15cm size (Note that is an average over total volume exploded, some pieces may be up to 2m in size down to less than 5cm). Violent Fragmentation (what the mining industry refers to as Crushing) would be uniform destruction to ~ 3cm. Pulverization would be uniform destruction to passing a 200 mesh screen - 0.0074cm.
- 302
- 46
I was mainly just explaining what I'm mostly sure blasters/miners consider the sizes involved to be. It should be noted, however, that Violent Fragmentation (Crushing) and Pulverization would be done by machines to further break down the particle size, so the powder factors would only be applicable for Fragmentation anyway.Spinosaurus75DinosaurFan said:
- 32,835
- 38,108
Not to mention that most of our frag feats don't involve isolated chunks anyway so it all breaks down to how stuff is destroyed for what Bambu already stated (Accuracy matters but in a place where it's not even close enough to make a meaningful difference and will cause more harm than good by applying to the wrong places, it really wouldn't work out), plus this is never gonna get solved even after the forum shift for what Bambu and Assalt have stated even if we do have the resources. Plus, toughness alone isn't gonna cut it, there's surface area and area of impact to consider too which are a whole new can of worms to deal with.
- 302
- 46
Is there a way to back-calc how much explosives you would need to achieve the three particles sizes using the Kuz-Ram model or something else that you would only have to solve once and then change depending on rock composition? [Where's a blasting engineer when we need one? I'm just a chemist.]
- 302
- 46
Could you solve this for Q then use X_m = .15m (15cm) for Frag, 0.03m (3cm) for V. Frag, and 0.000074m (0.0074cm) for Pulverization? Then adjusting your Rock Factor and Powder Factor to account for the rock composition?KLOL506 said:
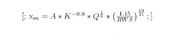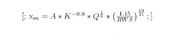
Anyway, managed to fix the LaTEX mess from jakuub's link and this is the formula for the particle size where:
x_m = mean particle size (cm)
A = rock factor,
K = powder factor (in kg/m^3)
Q = mass of explsovies (in kg)
RWS = relative weight strength of the explosive (Apparently blastex is used and its RWS is 0.84)
X_m= A*(K^-0.8)*(Q^0.167)*((1.15/0.84)^0.905)
Once you figure out your powder factor AKA mass of explosives multiply it with blastex's energy density of 740 cal/g or 3098232 J/kg of explosive used per cubic meter (I used this converter to convert from cal/g to joule/kg).
Rock factor and powder factor are apparently set and the mass of explosives is also apparently the same as powder factor.
Some powder factors here (Or just use the average of 0.75 kg/m^3 here, the other link gives almost equal values AFAIK but using separate rocks is better IMHO).
Though I should note that this doesn't work for stuff that isn't stone. AKA you can't use this for metal or wood. Rock factor is within 7-13.
Some more details about the Kuz-Ram model here
... Actually, the more I read, it seems like X_m changes depending on rock composition and/or uniformity index.
Nope. Big Nope. Way too complicated. I vote we leave it like it is.
- 11,392
- 13,145
You know I'm not going to pretend I possess great knowledge of what exactly you guys are talking about here, but I will say this:
At some point accuracy has to give in the face of practicality. We're ultimately just a bunch of people doing this for fun, and applying some insanely complex standards that ultimately limit our production output of calcs and generally slow that side of the wiki to a crawl, while making it far more awkward for anyone to pick up is just counterproductive.
We can afford simplification. We can't afford overcomplication.
At some point accuracy has to give in the face of practicality. We're ultimately just a bunch of people doing this for fun, and applying some insanely complex standards that ultimately limit our production output of calcs and generally slow that side of the wiki to a crawl, while making it far more awkward for anyone to pick up is just counterproductive.
We can afford simplification. We can't afford overcomplication.
- Status
