- 958
- 587
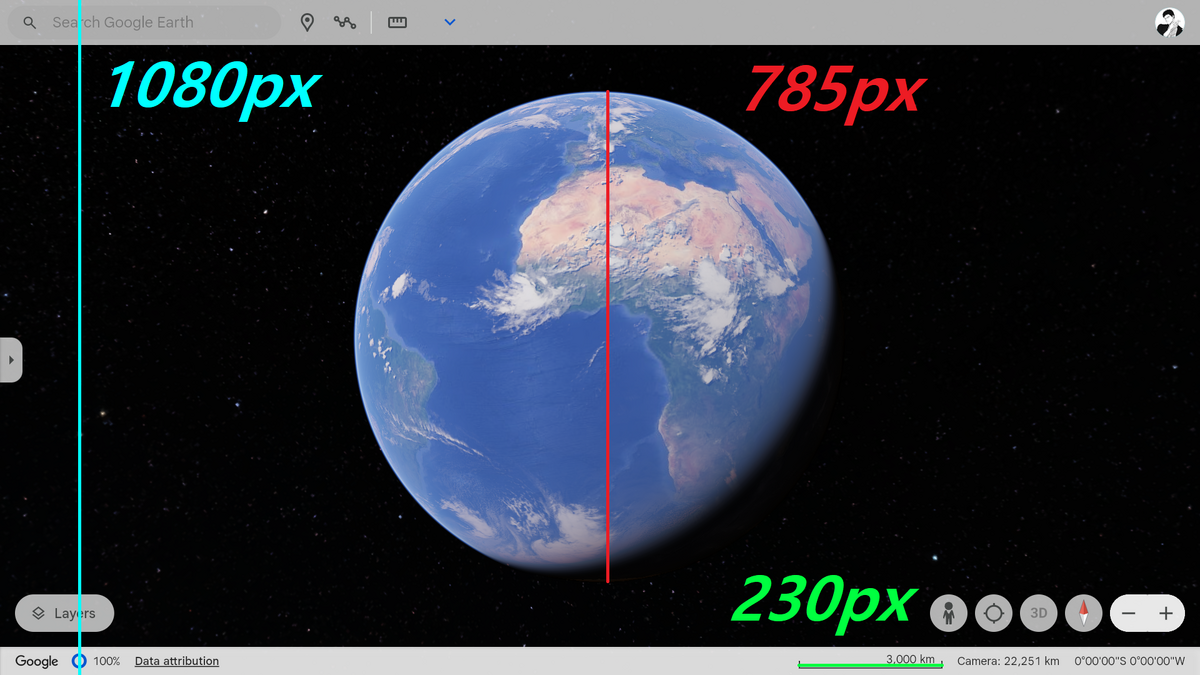
While trying to create a new angsizing formula for more accurate results, I discovered that Google Earth provides the distance from the camera to the ground and also includes scale lines indicating the length of objects on the screen. Using this information, I set out to develop a new formula. In the end, I modified the original formula to match the field of view used by the Google Earth camera.
I’d like to hear your thoughts on whether this formula could be implemented. I recalculated some cases using this new version and found that the distances were more than double those calculated with the original formula, which seems to be more accurate in most cases.
 vsbattles.fandom.com
vsbattles.fandom.com
Examples
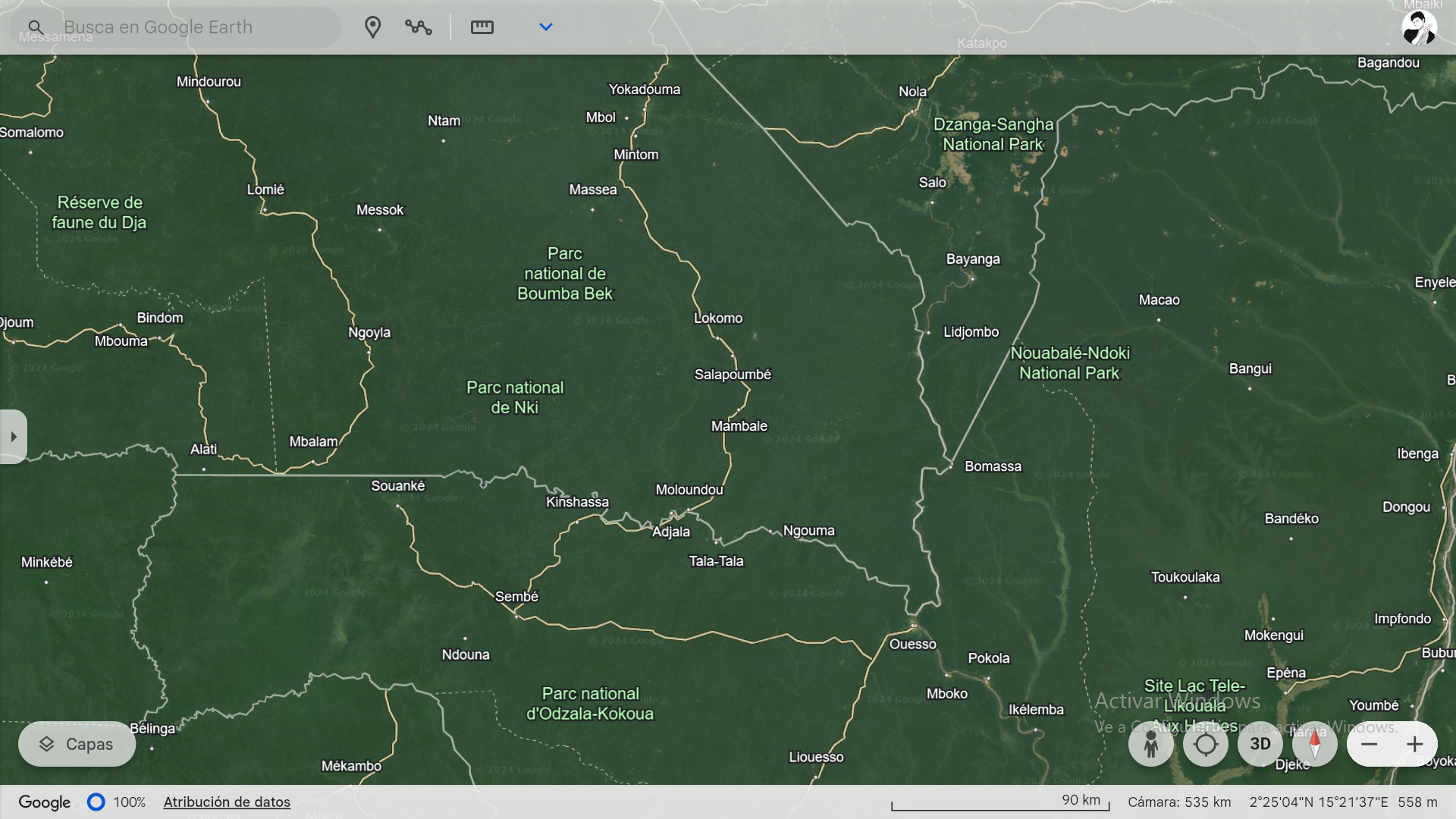
N°1

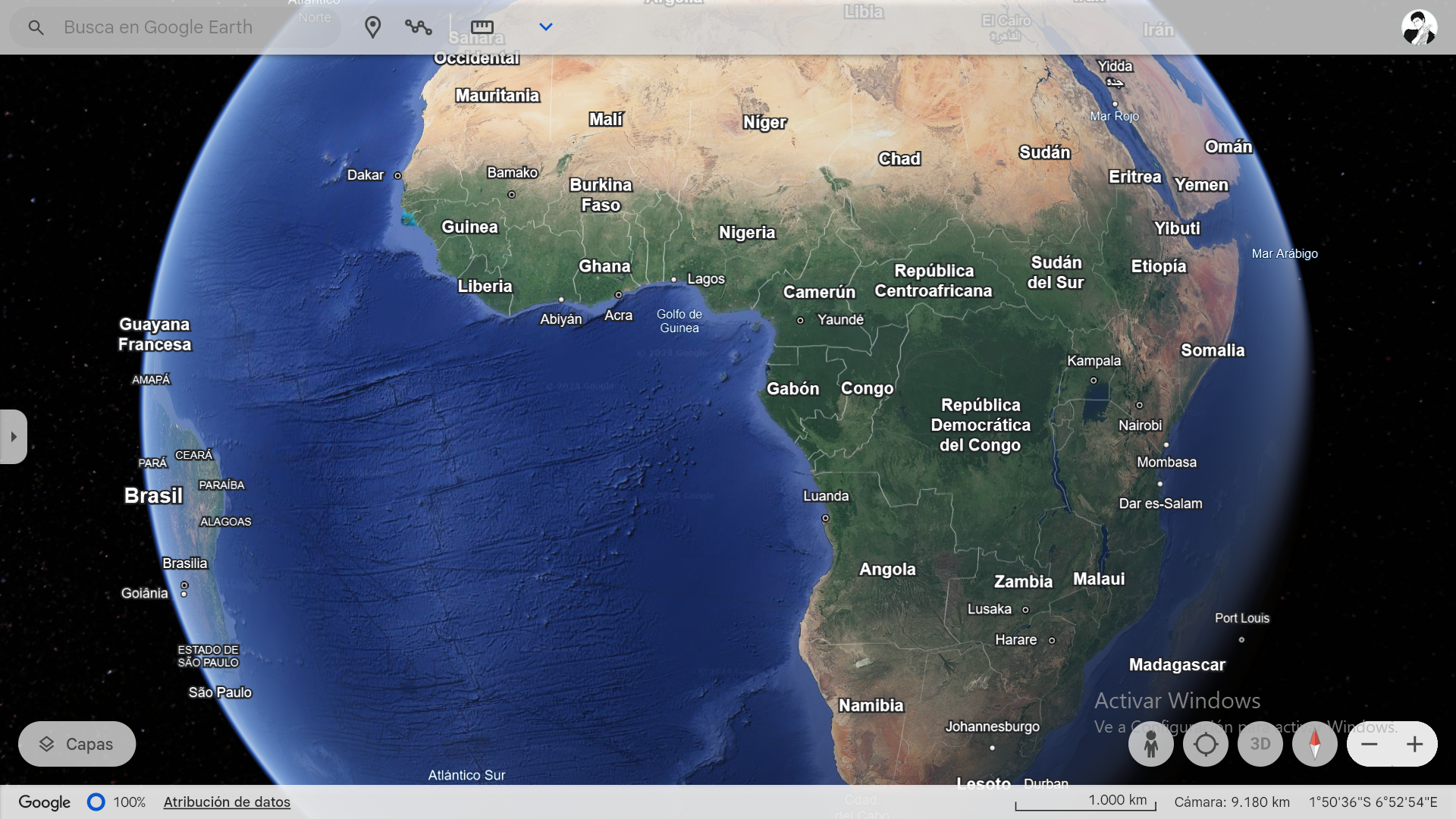
N°2

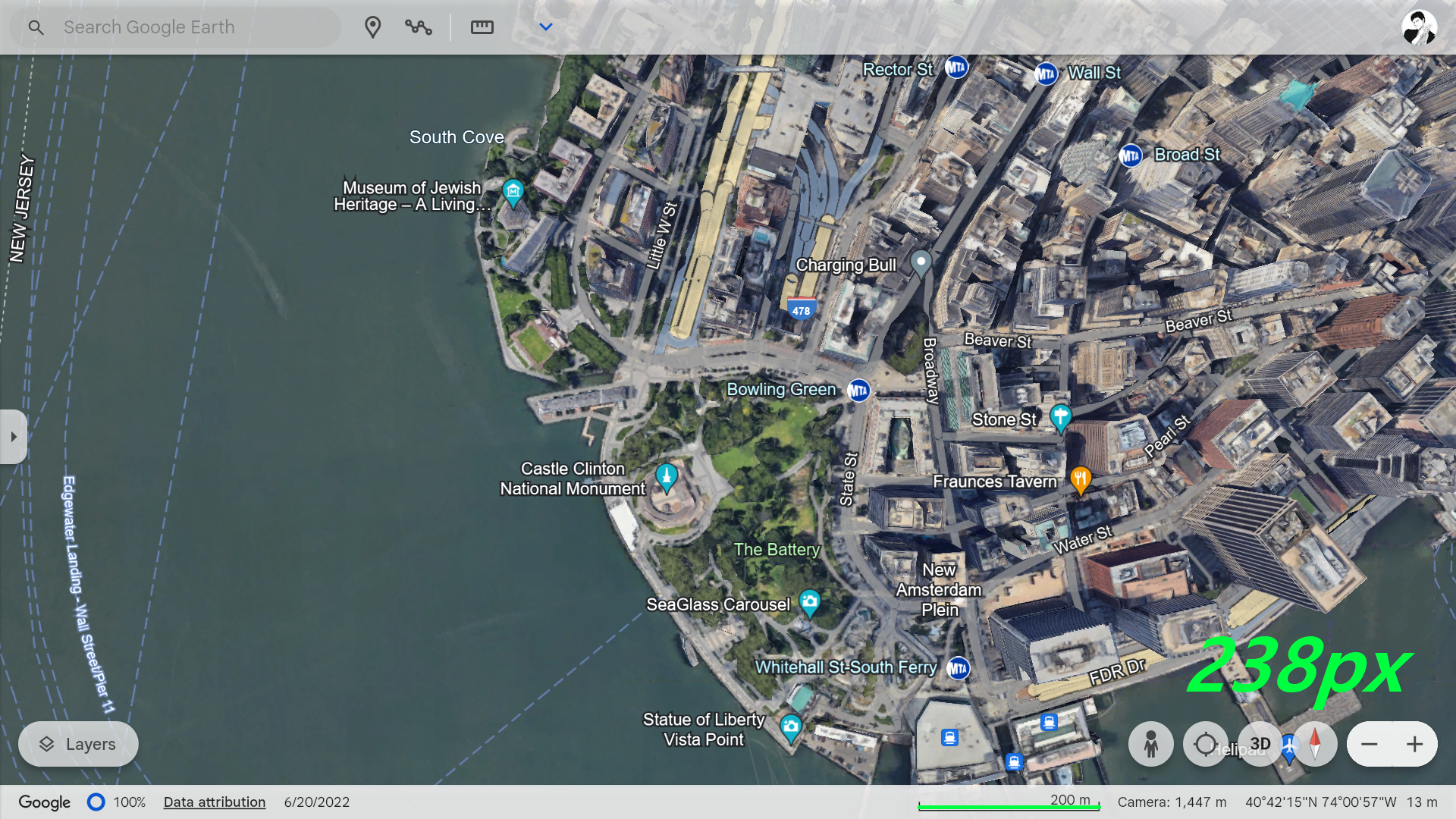
N°3

I’d like to hear your thoughts on whether this formula could be implemented. I recalculated some cases using this new version and found that the distances were more than double those calculated with the original formula, which seems to be more accurate in most cases.

Angsizing Formula 2.0
Examples
N°1

- 70deg: 12742 * 1080/(1411 * 2 * tan(70deg/2)) = 6,964 km
- 35deg: 12742 * 1080 / [1411 * 2 * tan (35deg/2)] = 15,466 km (-Radius = 9.095 km)
N°2

- Distance to Fire Flame 70deg: 0.2275 * 667 /(56 * 2 * tan(70deg/2)) = 1.93m
- Distance to Fire Flame 35deg: 0.2275 * 667 / [56 * 2 * tan (35deg/2)] = 4.29m
N°3

- Distance to Electro 70deg: 0.225 * 370 /(24 * 2 * tan(70deg/2)) = 2.47m
- Distance to Electro 35deg: 0.225 * 370 / [24 * 2 * tan (35deg/2)] = 5.5m
Last edited: