- 1,178
- 407
The problem
If an object is destroyed as a result of some attack we calculate the energy output of the attack using the original volume of the object and the destruction value of the material the destroyed object is made of. According to Naruto Forums (and that's the only source we have), the fragmentation value is equal to the shear strength of the material, violent fragmentation is equal to the tensile strength and pulverization is the compressive strength. But we never questioned the credibility of the source.
Fragmentation is defined as "the energy needed to make something fall apart in large fragment" while the definition of shear strength is "the strength of a material or component against the type of structural failure when the material or component fails in shear" As you can see those definitions do not line up quite well and the same reasoning can be applied to violent fragmentation and pulverization values as well. So there reasonably comes the question: "does this whole thing even make some sense?"
What should we do instead
The energy needed to destroy a particular object is indeed proportional to the original volume of the destroyed object however shear, tensile and compressive strength do not determine the amount of energy per unit volume. But there is a material property that does.
Toughness - is the amount of energy per unit volume that a material can absorb before rupturing.
Unfortunately, I couldn't find any toughness table for common materials. So how can it be calculated? Toughness can be determined by integrating the stress-strain curve by the following formula:
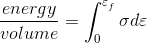
Where sigma is the stress and epsilo is the strain. f indicates the point of rupture.
Unfortunately, most materials have random stress-strain relation so it's really hard to find a function one can integrate. Hopefully, we can still measure it by measuring the area under the material's stress-strain curve using paint.net. You can also do the same thing with the load-displacement curve and then devide the result by the original volume of the specimen
(for those who found this page I can tell you that it's basically the same formula. Young's modulus is inversely proportional to toughness and there is 1/2 because the area under the elastic region has a shape of a right triangle via Hook's law)
Finding toughness for some common materials
So now we need to find some of those values...
Concrete
Source: https://www.youtube.com/watch?v=dtvm7YNsSU0

Area under the curve: 18134 px20 MPa - 77 px
0.05% - 56 px
Toughness: 18134*(20/77)*(0.05/100/56) = 0.042 J/cm^3
Stone

Limestone:
area under the curve: 166400 px
1000 psi - 6.895 MPa - 77 px
0.0005 (unitless) - 129 px
Limestone's toughness: 166400*(6.895/77)*(0.0005/129) = 0.058 J/cm^3
Sandstone:
area under the curve: 71070 px
2000 psi - 13.79 MPa - 79 px
0.002 (unitless) - 112 px
Sandstone's toughness: 71070*(13.79/79)*(0.002/112) = 0.22 J/cm^3
Wood
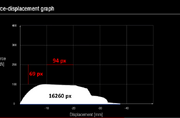
Source: https://www.youtube.com/watch?v=yqAFSKlALwkThe area under the curve: 16260 px
100 kN - 69 px
10 mm - 94 px
Work of deformation: 16260*(100/69)*(10/94) = 2507 J
The specimen is 25x10x15 cm wooden block so its volume is 3750 cm^3
Toughness: 2507/3750 = 0.67 J/cm^3
Soil
Source: www.youtube.com/watch?v=8hzizh7dB9A
There were 3 samples



1. Area 81492 px
0.05 MPa - 67 px
1% - 84 px
Toughness: 81492*(0.05/67)*(0.01/84) = 0.0072 J/cm^3
Using the same method sample 1 and sample 2 got 0.016 J/cm^3 and 0.011 J/cm^3 respectivily so I don't know which one should we pick
More Informatio
There are a couple of things people need to understand.
1. Toughness determines the minimal amount of energy required to rapture the material. There is no way we can find v.frag or pulv values using it. The best thing a can suggest is to set v.frag 10 times above the toughness and pulverization 10 times above v.frag. If anyone has a better idea I'm willing to hear it
2. This method is still not perfectly accurate. Idealistically the material needs to be completely solid and the impact needs to be perfectly flat and perpendicular to the surface of the destroyed object. But I guess we can ignore it because I believe it's the best we can do.
3. Pulverization value base on compressive strength can still be used for feats like this one because in order to make a hole like this one needs to compress the concrete inside the wall. The mechanical work of pressing this hole inside should be equal to the compressive strength times the volume.
If an object is destroyed as a result of some attack we calculate the energy output of the attack using the original volume of the object and the destruction value of the material the destroyed object is made of. According to Naruto Forums (and that's the only source we have), the fragmentation value is equal to the shear strength of the material, violent fragmentation is equal to the tensile strength and pulverization is the compressive strength. But we never questioned the credibility of the source.
Fragmentation is defined as "the energy needed to make something fall apart in large fragment" while the definition of shear strength is "the strength of a material or component against the type of structural failure when the material or component fails in shear" As you can see those definitions do not line up quite well and the same reasoning can be applied to violent fragmentation and pulverization values as well. So there reasonably comes the question: "does this whole thing even make some sense?"
What should we do instead
The energy needed to destroy a particular object is indeed proportional to the original volume of the destroyed object however shear, tensile and compressive strength do not determine the amount of energy per unit volume. But there is a material property that does.
Toughness - is the amount of energy per unit volume that a material can absorb before rupturing.
Unfortunately, I couldn't find any toughness table for common materials. So how can it be calculated? Toughness can be determined by integrating the stress-strain curve by the following formula:
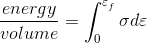
Where sigma is the stress and epsilo is the strain. f indicates the point of rupture.
Unfortunately, most materials have random stress-strain relation so it's really hard to find a function one can integrate. Hopefully, we can still measure it by measuring the area under the material's stress-strain curve using paint.net. You can also do the same thing with the load-displacement curve and then devide the result by the original volume of the specimen
(for those who found this page I can tell you that it's basically the same formula. Young's modulus is inversely proportional to toughness and there is 1/2 because the area under the elastic region has a shape of a right triangle via Hook's law)
Finding toughness for some common materials
So now we need to find some of those values...
Concrete
Source: https://www.youtube.com/watch?v=dtvm7YNsSU0

Area under the curve: 18134 px20 MPa - 77 px
0.05% - 56 px
Toughness: 18134*(20/77)*(0.05/100/56) = 0.042 J/cm^3
Stone

Limestone:
area under the curve: 166400 px
1000 psi - 6.895 MPa - 77 px
0.0005 (unitless) - 129 px
Limestone's toughness: 166400*(6.895/77)*(0.0005/129) = 0.058 J/cm^3
Sandstone:
area under the curve: 71070 px
2000 psi - 13.79 MPa - 79 px
0.002 (unitless) - 112 px
Sandstone's toughness: 71070*(13.79/79)*(0.002/112) = 0.22 J/cm^3
Wood

Source: https://www.youtube.com/watch?v=yqAFSKlALwkThe area under the curve: 16260 px
100 kN - 69 px
10 mm - 94 px
Work of deformation: 16260*(100/69)*(10/94) = 2507 J
The specimen is 25x10x15 cm wooden block so its volume is 3750 cm^3
Toughness: 2507/3750 = 0.67 J/cm^3
Soil
Source: www.youtube.com/watch?v=8hzizh7dB9A
There were 3 samples



1. Area 81492 px
0.05 MPa - 67 px
1% - 84 px
Toughness: 81492*(0.05/67)*(0.01/84) = 0.0072 J/cm^3
Using the same method sample 1 and sample 2 got 0.016 J/cm^3 and 0.011 J/cm^3 respectivily so I don't know which one should we pick
More Informatio
There are a couple of things people need to understand.
1. Toughness determines the minimal amount of energy required to rapture the material. There is no way we can find v.frag or pulv values using it. The best thing a can suggest is to set v.frag 10 times above the toughness and pulverization 10 times above v.frag. If anyone has a better idea I'm willing to hear it
2. This method is still not perfectly accurate. Idealistically the material needs to be completely solid and the impact needs to be perfectly flat and perpendicular to the surface of the destroyed object. But I guess we can ignore it because I believe it's the best we can do.
3. Pulverization value base on compressive strength can still be used for feats like this one because in order to make a hole like this one needs to compress the concrete inside the wall. The mechanical work of pressing this hole inside should be equal to the compressive strength times the volume.