Downgrade Self-Reference Engine

[Ovy7]

Looking at the main post, OP's translation is DeepL (i.e. literally MTL), so this entire "not official translation" discussion is pure lmfao

 

[Lewis]

First, it is explained here that there is a "highest rung" structure written here:

https://gyazo.com/990f70364e1e990e19bb65456b1301f3

I translated it to:

https://gyazo.com/5db58a2b7a2562157af8fe7b78e2186f

Then here is the culmination of the argument that ENGINE Self-Reference is Tier 0:

https://gyazo.com/3b924f4dadf475350d3148e284f856ba

official??

 

[LephyrTheRevanchist]

Looking at the main post, OP's translation is DeepL (i.e. literally MTL), so this entire "not official translation" discussion is pure lmfao

Amazing

 

[ImmortalDread]

As I said, peak debunk tho. I agree with everything!

 

[Ovy7]

That last pic, this one, is from the Viz translation.

Edit: but the other one is pretty much DeepL.

Edit2: DeepL's page, for reference:

Spoiler

vs

 

[Lewis]

Same :

 

[ImmortalDread]

Are we really required Ultima to comment here?

 

[Ovy7]

Yes, let him cook

 

[ShionAH]

Are we really required Ultima to comment here?

Yep

 

[Gasper]

Are we really required Ultima to comment here?

He brought the verse here so yes

 

[ImmortalDread]

Yes, let him cook

He is debunking the verse with DeepL, not sure.

 

[Ultima_Reality]

You are repeating the same argument, do you have no valid evidence other than this? You even argue that 巨大基数の階梯 is the same as hierarchy of different kinds of large cardinals, when it means only large cardinals with no context and transfinite progression to large cardinals.
Then I will fault your argument, climbing to the extreme highest peak in large cardinal numbers without context will only get hyper-inaccessible cardinals.

If you follow this logic, then the multiverse is still 0. There is quite a lot of things in-between hyper-inaccessibles and the smallest inaccessible cardinal.

For instance, if the smallest strongly inaccessible κ exists, then so does its power set, P(κ), which is obviously strictly larger than κ. Going by that route, there is also P(P(κ)), and P(P(P(κ))), and P(P(P(P(κ)))), and so on. However, none of those cardinals actually reach even the second inaccessible cardinal, because such a cardinal can't be the power set of any smaller number, and then after that (and the successors and power sets of the second inaccessible), there is the third inaccessible cardinal, and the fourth, and the fifth, and so on. And now think about how these are all still 0-inaccessibles, of which even the smallest 1-inaccessible is a limit and fixed point. And there's still the 2-inaccessibles, and then 3-inaccessibles, and then ω-inaccessibles. And then hyper-inaccessibles are κ-inaccessibles (Where κ is the aforementioned smallest inaccessible)

(A similar pattern is followed by weakly inaccessibles by the way)

And of course the multiverse is like, the bottom of an infinite hierarchy.

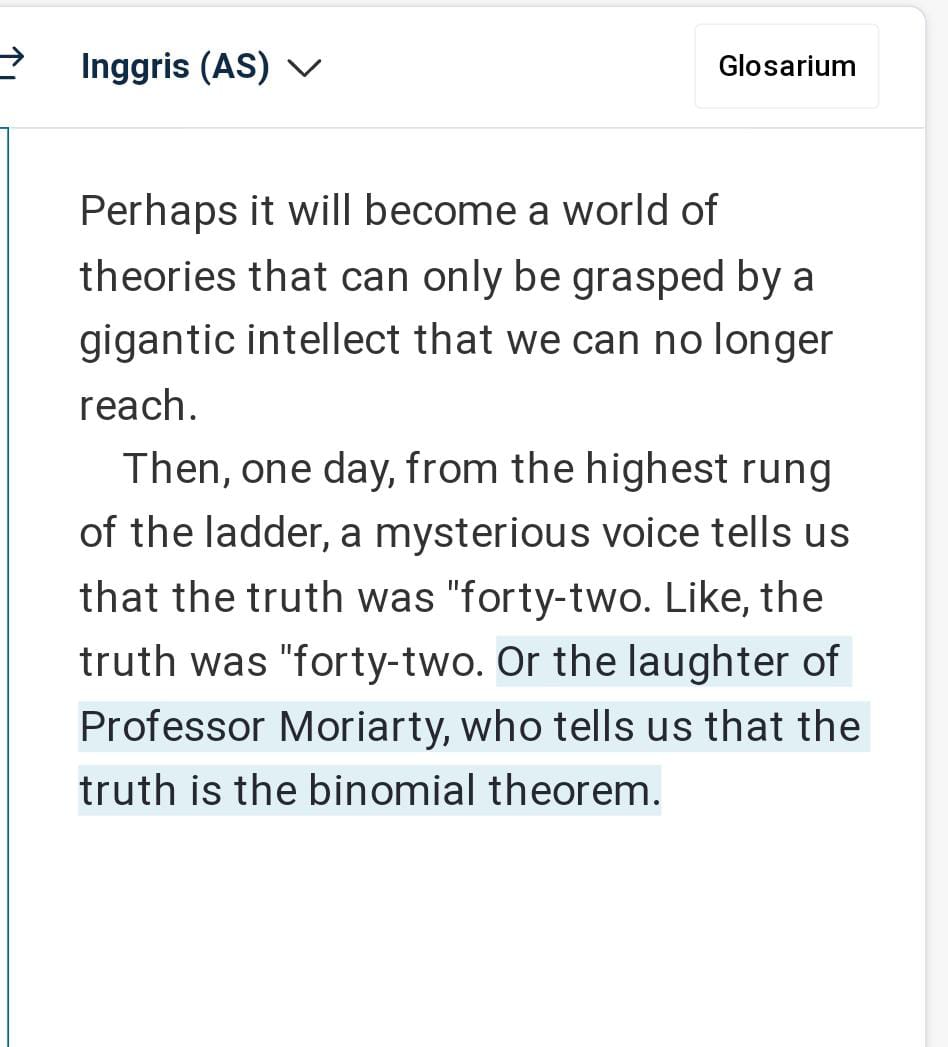
Anyway: I don't see what the point you're making in the OP is. The progression of theorems is one that first goes through natural numbers, and then into the infinite ordinals, and then it reaches the ladder of large cardinals. And then it also reaches the utmost limit of that ladder (The same term, 階梯, is used throughout that part of the text, and one directly follows the other, so the "ladder" whose limit is being reached here is obviously referring to the ladder of large cardinals), so much so that eventually things break down entirely and aren't even denoted by theorems or a progression of numbers anymore, just nonsense like "The truth is 42" or "Professor Moriarty laughs while him and Sherlock plummet down a waterfall."

 

[IdiosyncraticLawyer]

Ultima makes sense. Disagree with the OP FRA.

 

[Rakih_Elyan]

Ultima roast him.

Disagree.

 

[Rakih_Elyan]

For instance, if the smallest strongly inaccessible κ exists, then so does its power set, P(κ), which is obviously strictly larger than κ. Going by that route, there is also P(P(κ)), and P(P(P(κ))), and P(P(P(P(κ)))), and so on. However, none of those cardinals actually reach even the second inaccessible cardinal, because such a cardinal can't be the power set of any smaller number, and then after that (and the successors and power sets of the second inaccessible), there is the third inaccessible cardinal, and the fourth, and the fifth, and so on. And now think about how these are all still 0-inaccessibles, of which even the smallest 1-inaccessible is a limit and fixed point. And there's still the 2-inaccessibles, and then 3-inaccessibles, and then ω-inaccessibles. And then hyper-inaccessibles are κ-inaccessibles (Where κ is the aforementioned smallest inaccessible)

Also, scan for inaccessible k?

 

[Georredannea15]

Ehhhh... I think it's holding his Tier 0 position anyway. I disagree with OP on this but...

I'm neutral to other things. But even if their cardinal scale downgrades, they still stay at tier 0. So part of the OP is neutral and part of it I disagree.

And I guess the permanently inaccessible cardinals hold true here. But I don't know if it still scales to the all axiom system, but I guess the constant continuation of inaccessible cardinals... I guess it's scaling them.

Edit : So the large cardinals go on inifinite ordinals like "ladders" and every top ladder is a superset of the bottom ladder... it's with others... Yeah I guess it's okey... Man, what kind of cosmology is that?

 

[Lewis]

Also, scan for inaccessible k?

Vk+inaccessible cardinal

 

[Lewis]

This is scan.
It is said throughout plot that it is large cardinal than zfc+ and cardinal k

 

[Lewis]

what kind of cosmology is that?

Maybe..Ein sof

Edit:The Self Reference Engine, the "nothing" that functions as the driving force of "everything" via its continued operation (or perhaps non-operation). If you think about it in realist perspective—for example, "it's made up of a singular spacetime structure", this story becomes a very, very, very hard science-fiction

 

[Tooldyguy]

If you follow this logic, then the multiverse is still 0. There is quite a lot of things in-between hyper-inaccessibles and the smallest inaccessible cardinal.

Equivalent to sufficient evaluation, I only get that Self-Reference is a mahlo cardinal without any additions, as you said, it will still be 0, but it will drop considerably from the previous "encompassing all large cardinals" to now being a mahlo cardinal only. I dare to argue like this because like my previous argument, the large cardinal here really doesn't have a clear context to go towards "encompassing all large cardinals". If you have additional context, please explain to me.

 

[Tooldyguy]

This is scan.
It is said throughout plot that it is large cardinal than zfc+ and cardinal k

Bro where did you get this picture I even opened the book and there is no such sentence. Did you write it? I suspect

 

[Lewis]

There is no crazy person who has written a novel and explained each type of large cardinal. which we can assume is indeed a ladder of the List of large cardinal properties. and everyone listens to me This is fiction, not mathematical research.

 

[Lewis]

That last pic, this one, is from the Viz translation.

Edit: but the other one is pretty much DeepL.

Edit2: DeepL's page, for reference:

Spoiler

vs

Bro where did you get this picture I even opened the book and there is no such sentence. Did you write it? I suspect

Official???

 

[Lewis]

Bro where did you get this picture I even opened the book and there is no such sentence. Did you write it? I suspect

It doesn't appear in the story. But there are related words such as 巨大基数の階梯 which we have to find the meaning that the author wants to convey. Not to sit and find out if it's right or wrong.

 

[MrOMG]

Like lol. Even if the multiverse didn't have a ladder of cardinal numbers, Nemo Ex Machina would be level 0, it feels like this ladder of large cardinal numbers is the most important one, even though it was already clear that this ladder is just one of many other ladders. Like, even the ladder of large cardinals is a step in the ladder of alien mathematics (I'll even say that SRE is not a isolated book, there are others that reveal even more about cosmology, at least the Boys Surface, which also mentions alien mathematics).

 

[Lewis]

Thank you for helping out.

We only need one staff to close this thread (ovy7, Ultima disagree with OP.)

 

[Antvasima]

I will close this thread then. Thank you to everybody who helped out here.