Scaling from Planet Curvature

So this is about the practice in which one completes the circle of the shown curvature of earth in order to then scale something from the earth radius or similar practices. So basically what I have done for the explosion in this calc here for example.

Essentially I have thought about the practice a bit... and it is nonsense in my opinion.

Explanation incoming.

Distance of the Horizon circle if you look straight dow


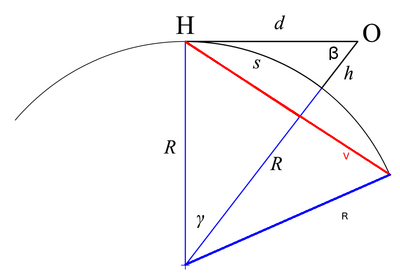
Let's look at the distance to the horizo article of wikipedia.

The angle y is connected to the earth Radius R and the Observer height h, by

$ cos (\gamma) = \tfrac{R}{R+h} $

The length of side V is, due to the law of cosines, given by

$ (V)^2 = R^2+R^2-2 \cdot R \cdot R \cdot cos(2 \cdot \gamma) $

and because of $ \gamma = cos^{-1}(\tfrac{R}{R+h}) $

we get

$ V = \sqrt{2 \cdot R^2-2 \cdot R^2 \cdot cos(2 \cdot cos^{-1}(\tfrac{R}{R+h}))} $

So what is V? Well, everything that lies between V and the Observer O would be the parts of earth that can in theory be visible. Or in other words if you look at the earth like this then V is the actual diameter of the part of earth visible to you.

To do a short plausibility check for that formula: For h=0 the horizon is exactly at the point the observer stands at (which is reasonable when modelling earth as a sphere) and for h>>R VÔëê2*R, which is also what is expected.

So most calcs that angsize from the fully visible earth diameter are likely still more or less correct, but for cases in which one had to complete the circle per hand it looks less good already.

Form of the Horizon circle, if you look at the horizo
Edit: I will try to redo this part with a better fundament sometime later, as I am not satisfied/certain with the amount of intuition necessary for this explanation currently.


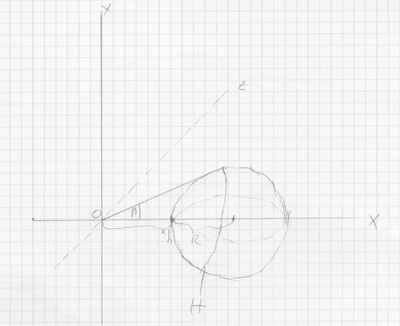
the drawing

I lack the formal knowledge to look at transformations of perspective mathematically, so I really am not quite sure about the following. What I did here is what I thought to seem like an intuitively correct approach on this problem and I will try to explain why, but it should be taken with a grain of salt. (also I am flying over some steps for details in the math here, I am not guaranteeing that I didn't miscalculate there (was a long calculation), but the conclusion should fit either way)
Let's for a moment disregard our eyes restriction of a limited Field of View and assume we are able to see 360┬░ around us.

If you think of it this way you will notice that turning you line of sight to another object doesn't change what you see. So one can say change of line of sight doesn't mean a change in what is theoretically visible from you current position.

That means if you turn your line of sight from straight down on the center of earth (like in the previous part) upwards to a point of the horizon, the position of the horizon stays the same line on the planet. (as you can also see from the calculation above)

Such a change of perspective can also be represented as a rotation around the Observer. That means if we put it into a coordinate system like in the drawing, we get the rotated version of the Horizon (marked with H in the drawing), by rotating it by the degree $ -\beta $ around the origin O. ($ \beta $ is given by $ \beta=\pi-(\pi/4+\gamma) $)

To further specify it mathematically: The Horizon H is given as $ H = Horizon := \{\phi \in \mathbb{R}^3\ |~||\phi||-d=||(R+h,0,0)-\phi||-R=0 \} $, where d is the distance shown in the graphic in the part above, and quantified as $ d=\sqrt{h \cdot (2R+h))} $.

H is a 1-dimensional Submanifold and as such one could find maps that cover it.

To be more specific for $ \psi (x) = (\sqrt{R^2-\tfrac{1}{4}V^2}, \tfrac{V}{2} \cdot cos(x), \tfrac{V}{2} \cdot sin(x)) $, $ \{((0,2\pi),\psi), ((-\pi,\pi),\psi) \} $ is an Atlas for H (because the triangle made by connecting V with O is an Isosceles triangle and the circle that is H has the radius V/2).

To rotate H so that we look at the horizon we want to rotate the whole thing by $ -\beta $, as already mentioned. This rotation can be visualized through the linear function

$ R_z(-\beta)= $

Where the table above is meant as a Matrix.

In order to get it as visualized in a photo we want to then project it unto a plain standing vertical to the x-axis. This done done through the function given by $ K_x (y_1,y_2,y_3)=(y_2,y_3) $.

So with that we can draw how the horizon looks in total for a given h. For example for h = 1 km it would look as seen in the following picture:


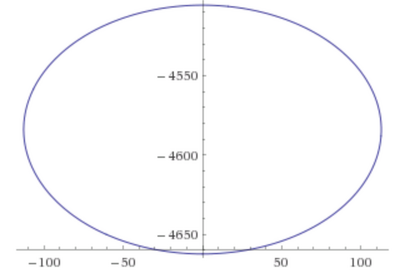
If you take into account that one can only see a small bit of the upper part that curve (due to the Field of View) you can see how the horizon would appear only slightly curved, like we are used to if we see it from such heights.

So if all those things are correct like I explained them, we have the second reason why scaling by completing the circle makes no sense: The horizon line actually doesn't create a circle but an ellipse.

Scaling background to foreground
Lastly we have a more simple argument.

If I were to calc this feat and scaled things from the earth in the background I hope all of you guys would tell me I'm stupid.

That is, because I would be scaling something that is depicted to be many kilometers in the background to something in the foreground. Such scaling would result in a heavy inflation on any size and distance scaled this way.

A similar thing applies if one scales something on the surface of the earth to the completed circle of the horizon. That is the case, because what one completes is the line of the horizon, which is often hundreds or thousands of kilometers behind the object you scale from (the precise distance it is away from the observer is d).

That alone is a very big reason why this method shouldn't work.

Conclusion
So all in all I have named what I believe are 3 flaws in the current method. The first point is easily solvable if you know the height of the observer (the formulas for that are as I have given), the second point is technically also solvable and the solution could be derived from the method I used here, but I think it probably is plenty difficult to practically do so for most people (you would have to figure out the function of the curve in a panel for that) and would likely not work in most cases, since the curves in mangas or comics are not drawn that precisely. The third is in theory probably also solvable, but I have no idea how and it would likely be dependent on first having to solve problem 1&2 in order to solve that, even if one knew how it is done.

So in practical terms that means that, if it is agreed that my arguments are legitimate, we likely can not use such a method to scale things any more.


So: What do you think, everyone?

Soo, basically, accepted calcs that uses such scaling are going to be null if this is accepted?

Yes, pretty much. Though calcs were the earth is viewed from a large height, like for example in the Irene calc, would likely be unaffected by this, as in that case h>>R, so that VÔëê2*R.

bump?

I've highlighted the thread but at the moment my brain is too fried to check anything.

Bump.

The calc team members should give their thoughts on this.

Would something like Kerrigan's feat be called into question under this?

Well, from a practical angle, we do not have the resources to start to search for and revise all calculations that have used this method.

Also, would the above text become a new calculation instruction page, or should we inform our community about the standard in some other manner?

If such method of calcuation would be rendered unusable due to this, is there any other way to evaluate them?

Yes. If we have no other reasonable way of calculating such feats, I do not know if we have any other choice than to continue using it.

Well, the practicle implementation of such a change is as always something too time consuming to do it at once, I suppose.

One could consider doing it gradually like suggested for some projects in the past (maybe putting a note about it on the community page), though that will also have the usual drawbacks.


In regards to an alternative: For some of the calcs one could probably figure out some other scalings, but I don't know a general purpose method to for all of them. (maybe some calc group member has a clever idea?)

Well, there are several prioritised other projects lined up, and I do not think that we could demand this much extra work from the calc group members, and the rest of the staff for no practical gain.

We would first have to sift through a large part of our profile pages to see which ones that scale from this method, then redo the connected calculations, with no obvious easily manageable alternative, and finally rescale all of the connected pages for all of the verses in question.

We have a hard enough time managing the rescaling of a single verse at a time.

In addition, the OBD/Narutoforums would still use this method, so we would not be able to use a lot of their calculations in the future.

In conclusion, with all due respect for all of your help to this wiki, I think that this may overcomplicate matters, and unreasonably tax our already strained resources in combination.

Hmm... ok.

Would you mind the thread staying open for a bit? Since I would non the less be interested in opinions on wether my doubts about the method are even justified from a purely theoretical standpoint.

Yes. That is fine. Regrettably, it simply seems unrealistic to apply your standards in practice.

For the...

Scaling background to foreground
Looking at this example of a planet shown here, we are actually scaling the foreground to the background of said planet, not the other way around. This would mean that if you drew a perfect circle where a section of a planet is shown, such as this picture:


The completed circle would actually look like this...


Which is similar in shape compared to the picture shown below.


As for why we draw a perfect circle for partially shown planets, we are trying to trace what the shape of a planet would look like, based on the shape of the curvature shown on the partially shown planet.

Now, for angsizing a landmass from a partially cut planet, I agree that the method used for that is rather iffy. Will cover in the next post however.

Note that your theory regarding curvature where the curve of the planet is shown to be on Earth instead of outer space, such as this example here, then utilizing planet curvature, in this case, would be iffy at best.

As we can clearly see in the picture that if we used curvature scaling, the size of the actual planet itself would be way smaller compared to its atmospheric layer in this case, which is highly unlikely.

Btw...

$ cos (\gamma) = \tfrac{R}{R+h} $

About this equation, are you using "degrees" or "radians" to calculate the actual value of the gamma?

Thank you for the help with sorting this out Lina.

Should be radians if I did it correctly.


Regarding scaling size of the planet from things on the planet: For that my first and third point don't apply. This thread was initially only written for scaling objects from the size of the planet, so that wasn't what I had in mind with those points.


The second point should apply for both, though.

For the second point your example isn't a counterexample as you didn't chose the line of sight to be pointed towards the horizon line, as I assume in the second point, but in the image you chose it is focused on the earth center. So it doesn't fulfill the axiom of point 2 or, if we generalize the argument in point 2 a bit further, it is the special case for which $ \beta = 0 $. Hence no perspective transformation happens, so that for that case the method I describe also happens to predict a circle.

But all in all I think I might be able to bring the point 2 in a better proven version by using some formulas for computer simulation of view. (I think this article looks promising it that regards)

But I will need time to properly work on that and don't have it anytime soon, so I will not press that point for now.

Well, we still need a workable formula that the calc group members can use for these types of calculations. If it can only be done by specific computer simulation programs, we would not be able to use such feats any more, which is not practically feasible.