• This forum is strictly intended to be used by members of the VS Battles wiki. Please only register if you have an autoconfirmed account there, as otherwise your registration will be rejected. If you have already registered once, do not do so again, and contact Antvasima if you encounter any problems.

    For instructions regarding the exact procedure to sign up to this forum, please click here.
  • We need Patreon donations for this forum to have all of its running costs financially secured.

    Community members who help us out will receive badges that give them several different benefits, including the removal of all advertisements in this forum, but donations from non-members are also extremely appreciated.

    Please click here for further information, or here to directly visit our Patreon donations page.
  • Please click here for information about a large petition to help children in need.

Galaxy busting: the calc?

I'm not sure what you mean. Do you want an example of what kind of calculation can yield galaxy results? The joule count is the value required to destroy a galaxy.
 
I'm not sure if it has a specific calculation. I believe it was derived from being able to destroy all planets and stars over a diameter of 100,000 light years.
 
I tried to recreate the calc. But I wasn't able to do so. I am getting 10^83 joules for destroying a galaxy whereas the AP is listed as something 10^66 joules.

I'm using the square inverse method:

x / (6.276*10^41 joules) = (4.7304*10^20 meters)^2 / (1 meter)^2
 
Pretty sure in the Attack Potency page you can find this link that cotains the calc for Solar System level and above, including Galaxy level.
 
What Dziga said. The calc itself is actually very simple. It just finds the radius of the Milky Way, then uses that to calculate a sphere, then compare the sphere's dimensions to the suns, and times the GBE of the sun by the dimensions.
 
Darkanine said:
What Dziga said. The calc itself is actually very simple. It just finds the radius of the Milky Way, then uses that to calculate a sphere, then compare the sphere's dimensions to the suns, and times the GBE of the sun by the dimensions.
Click to expand...
Nani?
 
Is that compensating for dark energy/matter? I don't think a sphere with the galaxy's dimensions would be accurate...
 
The energy we use to destroy the Galaxy is simply an omnidirectional explosion that involves the entire galaxy. To determine its energy, place Sun at the edge of the Milky Way and then calculate the energy to destroy it by an omnidirectional explosion from the center of the Milky Way. It's just a inverse square law calculation, it's quite simple if you stop to think.
 
Wait. I'm not understanding this calc at all. It uses Area but that's two dimensional. Shouldn't destroying a galaxy be three dimensional

Here it is:

Spherical:
Radius Milkyway: 4.7305E+20 m (50000 ly)

Area the explosion has to cover: 4 * ¤Ç * (4.7305E+20 m)^2 = 2.812055951925949131e42 m^2

Frontal area of sun: ¤Ç * (696342000 m)^2 = 1.5233337134996349872e18 m^2

Energy to destroy Galaxy:

(2.812055951925949131e42 m^2 / 1.5233337134996349872e18 m^2) * 6.87*10^41 J = 1.2681938447583566593e66 J
 
Inverse Square Law is something for every unit area of a sphere. It is an idea that is the basis for many laws like the Law of Colomb and the Law of Gravity.
 
I just do not understand why to use ¤Ç . I did all the calculation again to find the formula summarized and in all of them the ¤Ç of the Inverse Square Law is canceled with the ¤Ç of the contact area.
 
Yes use. Lei do Quadrado Inverso

I (In this case it will be Joule / m┬▓) = Energy / 4¤ÇRt┬▓

I x 4¤ÇRt┬▓ = Energy

I is this case will be the energy to destroy the Sun per area unit (In this case we consider the area of impact that is determined by ¤Çr┬▓): GBE / ¤Çr┬▓

Rt is the total radius of the explosion.

r is the radius of the targect.

Then:

Total Energy = GBE x 4 x (Explosion Radius/Target Radius)┬▓
 
Intensity is only an application of the Inverse Square Law and not the basis of the idea. What is being used in this case is the dissipation principle of something in this case the dissipation energy of an omnidirectional explosion.
 
Alright.

I'm still not following.

The forumla is

I = S/4(pi)R^.

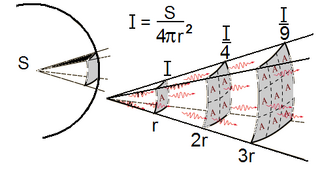
I = the GBE of a star

S= the energy output

4pir^2 = the Area of the explosion

r itself is the raidus of the galaxy

Where do you get target radius from? and how does that play in the equation?
 
I is not the GBE of the star, it is the energy per unit area. In this case it will be the energy per unit area in a given radius, in which case it will be the energy that is needed to destroy the target by area. This area will be minimally the cross-sectional area of the target which in the case of a sphere is pi x r ^ 2. With this information we know that I will be GBE / (pi x r ^ 2).
 
I'm sorry. I'm still just can't follow this. Forgive me for being a bit dense. But how could I not be the GBE?

I is what the source of power will be at r distance. The calc is to see how much power will it take to destroy the sun at r distance.

r being 50000 Light years

From the wikipedia page:

https://en.wikipedia.org/wiki/Inverse-square_law

Let the total power radiated from a point source, for example, an omnidirectional isotropic radiator, be P. At large distances from the source (compared to the size of the source), this power is distributed over larger and larger spherical surfaces as the distance from the source increases. Since the surface area of a sphere of radius r is A = 4¤Çr 2, then intensity I (power per unit area) of radiation at distance r is

In our case, P and S are the same

The calc here seems to add an extra step of dividing the surface area of the sun by the surface area of the galaxy sphere but, I don't understand why that step is added.
 
Something / Area is the principle of the Inverse Square Law am I right? In this case, as we speak of an explosion, the context of the Inverse Square Law will be the energy per unit of area. This will be our I. Being so the unit of measure of I will be J / m┬▓.

With this we know that we need something to be destroyed, in this case a star. The energy needed to destroy this is your GBE and it will be divided by the cross sectional area of the star (Pi x r┬▓). Therefore:

I = GBE / (Pi x r┬▓) = Total Energy / (4 x pi x Rt┬▓)

Thus: Total Energy = GBE x 4 x (Rt / r) ┬▓
 
"With this we know that we need something to be destroyed, in this case a star. The energy needed to destroy this is your GBE and it will be divided by the cross sectional area of the star (Pi x r┬▓). "

I think this is the confusion. It shouldn't get divided. Every meter square of the surface area at distance R will be measured as I.
 
Yes. That's right.

I think I figured out what the original calc was trying to do. Using the square inverse law, ever meter square at 50,000 lys will hold enough energy to destroy a star. However stars are not that small. They're ginormous. So they tried to compensate for this by dividing that cross section. However. I believe that method to be a faulty method to solve this issue of over power.

A better method would be a simple equalization:

GBE of the Sun / an area that covers the entirty of a star* = x/ 1

Then Solve for x

then take x and use that for I

I = S/4(pi)r^2.

where

S is the total power of the energy

I is energy per meter square

r is the raidal distnace


* for the area that covers the entirety of a star, I would suggesst takeing the diameter of the sun which is 1.989×1030 kilograms or 1.989*10^33 meters

Take that diamter and square it to get 3.956121*10^66 meters squared for an entire square area that covers a star


To put this entire thing into work:

GBE of the Sun / an area that covers the entirty of a star* = x/ 1

6.87*10^41 J / 3.956121*10^66 m^2 = x/ 1 m^2

which would give

522344051.387739 J per square meter


Then plug that into the the Inversquare law equation for I

I = S/4(pi)r^2.

522344051.387739 = x / 4(pi)(473036523629040000000^2)

which would give

1.4687770092818*10^51 Joules for the S.

That would be how much power it would take to destroy every star in a radius of 50,000 light years

Much lower number than what it was before.
 
Iamunanimousinthat said:
Just some additon: the reason why I think the original calc was faulty because of it's cross section division becasue it took the entire surface area of the star but realistically, only half the star will receive the damage of the explosion at a time, not its' entire surface area.
Click to expand...
Wait not. I'm wrong. They did use the front face of the sun. What they did was divide the area of the galaxy with the area of the sun's face and then times that with the GBE of the sun. This didn't utilize the inverse suqare law equation at all.
 
This is not the diameter of the Sun, look at the unit that is the mass of the Sun. The diameter of the Sun is 1391400 km or 1391400000 m. And you can not simply square because as the sun has a spherical shape the area of impact will be minimally the area of a circle with the same radius. In this case the area will be 1.5205261e18 m┬▓

Then: I = 6.87e+41 / 1.5205261e18= 4.51817302e23 J/m┬▓.

I = Total Energy / 4 x pi x 4,73037e+20┬▓

Total Energy = 4.51817302e23 x 4 x pi x 4,73037e+20┬▓ = 1.2704657e+66 Joules.

And it's not the whole area being used, you must be confusing with the surface area of a sphere that is 4 x pi x r┬▓. It would actually be only half of it that would be hit, but to use that we would have to consider that every m┬▓ of the sun's will also receive the same energy, not to be limited to that we use the cross-sectional area of a sphere. In this case we will not have to divide by 2 because we use the whole cross-sectional area in impacts just as it does with friction calculations. We use the information on this page as the basis.
 
This is the basic principle of the Inverse Square Law, they take the energy per area that will be needed to explode a star and multiply by the surface area of the explosion. This is rather Inverse Square Law, the procedure is the same.
 
You're completely right. I typed in diamter of the sun and the search engine gave me the mass of the sun. I didn't even notice until I just double checked it. ( i was wondering why it was so low)

Let me do everything again: and use the cirlce area instead of squaring the diamter


To put this entire thing into work:

GBE of the Sun / an area that covers the entirty of a star* = x/ 1

6.87*10^41 J / 1520526100532553 = x/ 1 m^2

which would give

4.5181730176112*10^26 J per square meter

Then plug that into the the Inversquare law equation for I

I = S/4(pi)r^2.

4.5181730176112*10^26 = x / 4(pi)(473036523629040000000^2)

which would give

1.2704631429408*10^69 Joules for the S.

Which would be a bit higher than what's listed already. But about similiar (in terms of exponential amounts)
 
You must log in or register to reply here.

Similar threads

Hasty12345
Absolute Zero and Attack Potency Question
Replies
2
Views
733
Hypertornado099
Hypertornado099
ArachDusa
Would destroying Jupiter be a 5-A+ feat?
Replies
1
Views
1K
KLOL506
KLOL506
StalkerCh
Spational manipulation or attack potency ?
Replies
0
Views
768
StalkerCh
StalkerCh
  • Locked
Why can't characters be assigned a 5-C tier without calculations?
Replies
32
Views
3K
Antvasima
Antvasima
BOEGVELD
Legend of Korra calcs
Replies
1
Views
416
Maizesoup
Maizesoup
Back
Top