- 54
- 13
So i have a big doubt regarding a statement from this page:
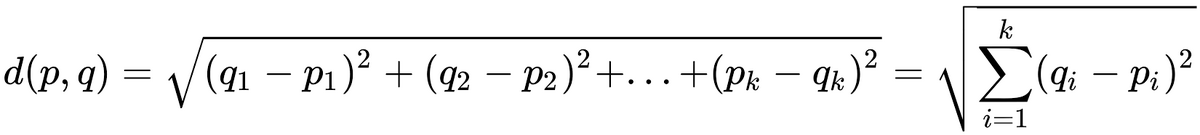
 vsbattles.fandom.com
vsbattles.fandom.com
Which is:
Assuming continuum hypothesis as true(since p(ℵ0) is also taken as ℵ1) wouldn't p(p(ℵ0)) just be ℵ2?
Since p(ℵ0) is 2^ℵ0 which is ℵ1, so p(p(ℵ0)) would just Be 2^ℵ1 which would be ℵ2?
And shouldn't that amount of universes be 6D since ℵ1 universes is 5D?
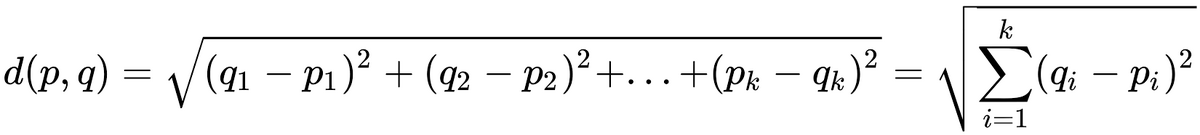
Tiering System FAQ
A: Whether higher-dimensional entities qualify for such high tiers or not depends on several different factors, which may take root both in and out-of-verse. To explain this situation, we must first clarify what exactly being higher-dimensional entails. In a way, yes, though not how most would...
Which is:
However, the same does not apply to sets of higher cardinalities than this (Such as P(P(ℵ0)), the power set of the power set of aleph-0), as they would be strictly bigger than all of the spaces mentioned above, by all rigorous notions of size, regardless of what their elements are (Points, universes, dimensions, etc). From this point and onwards, all such sets are High 1-B+
Assuming continuum hypothesis as true(since p(ℵ0) is also taken as ℵ1) wouldn't p(p(ℵ0)) just be ℵ2?
Since p(ℵ0) is 2^ℵ0 which is ℵ1, so p(p(ℵ0)) would just Be 2^ℵ1 which would be ℵ2?
And shouldn't that amount of universes be 6D since ℵ1 universes is 5D?