Osmium Mountain and Neutronium Mountain

[Rockysavannah]

In 1997, Rheasilvia, the most prominent surface feature on the asteroid Vesta, was discovered in Hubble Space Telescope images. The peak rises 20―25 km (12―16 mi) from its base, making it the highest mountain in the Solar System.


I've taken the liberty of calculating hypothetical mountains composed of osmium and neutronium, standing at the same height and shaped as a perfect Three-Dimensional cone and has its peak & corners have the angles of an equilateral Two-Dimensional triangle.









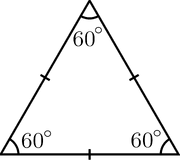
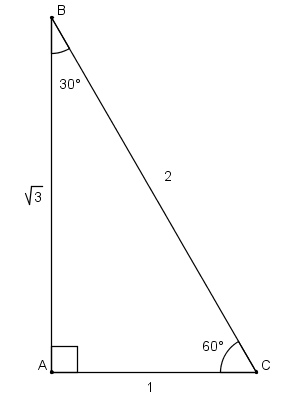
Length of 1/2 of equilateral triangle base: (25 km * sin (30┬░))/sin (60┬░)= 14.43375673 km


Length of equilateral triangle base: 14.43375673 km × 2 = 28.86751346 km





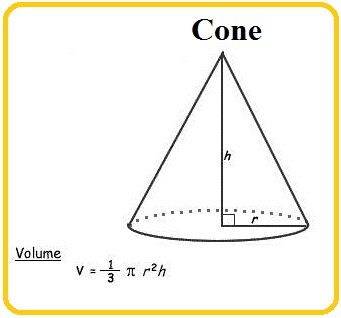
Volume of cone: 1/3 ├ù ¤Ç ├ù (14.43375673 km)2 ├ù 25 km = 5454.153913 km3


Density of Osmium: 22.59 g/cm3


Density of a Neutronium : 4 × 1017 kg/m3


Conversion of Density of Osmium from g/cm3 to kg/km3: 22,590,000,000,000 kg/km3


Conversion of Density of a Neutronium from kg/m3 to kg/km3: 3.9999999999999995 × 1026 kg/km3


Mass of osmium mountain: 22,590,000,000,000 kg/km3 × 5454.153913 km3 = 1.232093369 × 1017 kg

Mass of neutronium mountain: 3.9999999999999995 × 1026 kg/km3 × 5454.153913 km3 = 2.181661565 × 1030 kg


I'd like to find out how much force it would take to destroy these mountains.

 

[Antvasima]

If it is not related to any actual character feat, it is better to ask elsewhere than in this wiki.

 

[Rockysavannah]

Oh, ok.